Tag: Best NCERT Solutions

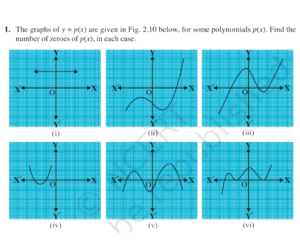
How to find number of zeroes from a graph

• A zero (root) of $p(x)$ is an $x$-value where $y=p(x)=0$ — i.e., where the graph meets the x-axis.

• Count the distinct x-axis intersection points:

  • If the graph crosses the x-axis at a point → that counts as one distinct zero.

  • If the graph just touches the x-axis and turns around there (tangent) → that counts as one zero (a repeated/double root).

  • If the graph never meets the x-axis → zero real zeroes.

  • If the graph meets the x-axis at $n$ distinct points → there are $n$ real zeroes (max $n$ for degree $n$).

Common examples (so you know what to look for)

• Straight line crossing x-axis once → 1 zero.

• Parabola crossing x-axis twice → 2 zeroes.

• Parabola tangent to x-axis (touches once) → 1 zero (double).

• Cubic curve that crosses three times → 3 zeroes.

• Curve entirely above/below x-axis → 0 zeroes.

• Higher-degree curve crossing 4 separate times → 4 zeroes.

(There’s an earlier worked example in the book — Fig. 2.9 — where the answers were: (i)1, (ii)2, (iii)3, (iv)1, (v)1, (vi)4. That’s the same idea you’ll apply to Fig. 2.10.)