Go Back to CLASS 11TH PHYSICS Page

Question 2.10

A man walks on a straight road from his home to a market 2.5 km away with a speed of 5 km h⁻¹. Finding the market closed, he instantly turns back and walks home with a speed of 7.5 km h⁻¹.

Find:

(a) Magnitude of average velocity
(b) Average speed

for the time intervals:
(i) 0 to 30 min, (ii) 0 to 50 min, (iii) 0 to 40 min

---

Given

• Distance to market = 2.5 km

• Speed while going = 5 km h⁻¹

• Speed while returning = 7.5 km h⁻¹

---

Step 1: Time taken in each part

Time to reach market

 

$$t_1=\frac{2.5}{5}=0.5\text{h}=30\text{min}$$

Time to return home

$$t_2=\frac{2.5}{7.5}=\frac{1}{3}\text{h}=20\text{min}$$

Total time for complete journey

$$t_{\text{total}}=30+20=50\text{min}$$

---

(i) Time interval: 0 to 30 min

During this time, the man only walks towards the market.

Displacement

$$=2.5\text{km}$$

Total path length

$$=2.5\text{km}$$

(a) Magnitude of average velocity

$$=\frac{2.5}{0.5}=5{\text{km h}}^{-1}$$

(b) Average speed

$$=\frac{2.5}{0.5}=5{\text{km h}}^{-1}$$

 

---

(ii) Time interval: 0 to 50 min

The man goes to the market and returns home.

Displacement

$$=0(\text{initial and final positions are same})$$

Total path length

$$=2.5+2.5=5\text{km}$$

(a) Magnitude of average velocity

$$=\frac{0}{50\mathrm{/}60}=0$$

(b) Average speed

$$=\frac{5}{50\mathrm{/}60}=6{\text{km h}}^{-1}$$

---

(iii) Time interval: 0 to 40 min

• First 30 min: reaches market

• Next 10 min: returns home

Distance covered in 10 min return

Speed = 7.5 km h⁻¹
Time = 10 min = 1/6 h

$$\text{Distance}=7.5\times \frac{1}{6}=1.25\text{km}$$

Position after 40 min

$$2.5-1.25=1.25\text{km from home}$$

Displacement

$$=1.25\text{km}$$

Total path length

$$=2.5+1.25=3.75\text{km}$$

(a) Magnitude of average velocity

$$=\frac{1.25}{40\mathrm{/}60}=1.875{\text{km h}}^{-1}$$

(b) Average speed

$$=\frac{3.75}{40\mathrm{/}60}=5.625{\text{km h}}^{-1}$$

---

Question 2.11 

In Exercises 2.9 and 2.10, we distinguished between average speed and magnitude of average velocity. However, no such distinction is required for instantaneous speed and instantaneous velocity. Why? Explain.

---

Answer

Key Idea

The difference between speed and velocity arises because they are defined over a finite time interval. But instantaneous quantities are defined at a single instant of time.

---

Definitions

Instantaneous velocity

Instantaneous velocity at a given instant is defined as:

$$\vec{v}=\underset{\mathrm{\Delta }t\to 0}{\lim }\frac{\mathrm{\Delta }\vec{x}}{\mathrm{\Delta }t}$$

It has both magnitude and direction.

---

Instantaneous speed

Instantaneous speed is defined as:

$$\text{Instantaneous speed}=\underset{\mathrm{\Delta }t\to 0}{\lim }\frac{\text{distance travelled}}{\mathrm{\Delta }t}$$

It has only magnitude, no direction.

---

Why are they always equal in magnitude?

• Over an infinitesimally small time interval (Δt→0):

  • The distance travelled becomes equal to the magnitude of displacement.

  • There is no change of direction in that tiny interval.

• Hence,

$$\text{Instantaneous speed}=\mathrm{\mid }\text{Instantaneous velocity}\mathrm{\mid }$$

Why the distinction disappears

• For average quantities, the particle may:

  • change direction,

  • retrace its path,

  • or return to the starting point.

• For instantaneous quantities, motion is examined at a single point in time, so:

  • path length = displacement (in magnitude),

  • speed = magnitude of velocity.

---

Question 2.12 

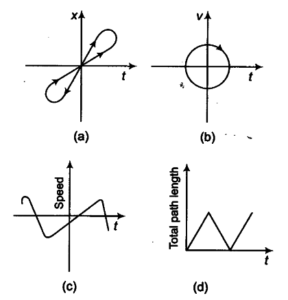
Look at the graphs (a) to (d) (Fig. 2.10) carefully and state, with reasons, which of these cannot possibly represent one-dimensional motion of a particle.

---

Answer:

In one-dimensional motion:

1. At a given instant of time, a particle can have only one position.

2. Speed can never be negative.

3. A graph must satisfy the physical meaning of the quantities on the axes.

---

(a) – Possible

• This graph represents a particle moving forward and then backward.

• At every instant of time, there is only one position.

• ✔️ Physically possible in one-dimensional motion.

---

(b) – Not Possible ❌

• This graph shows more than one position for the same time.

• A vertical line cuts the graph at more than one point.

• This means the particle is at two positions at the same time, which is impossible.

Cannot represent one-dimensional motion.

---

(c) – Possible

• This graph represents motion where speed increases and then decreases.

• Speed remains positive throughout.

• ✔️ Physically possible.

---

(d) – Not Possible ❌

• This graph shows negative values of speed.

• Speed is a scalar quantity and cannot be negative.

• Negative values have no physical meaning for speed.

Cannot represent one-dimensional motion.

---

Question 2.13 

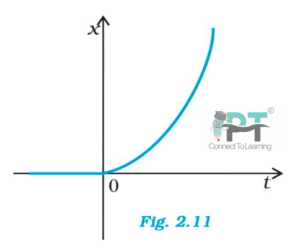
Figure 2.11 shows the x–t plot of one-dimensional motion of a particle. Is it correct to say from the graph that the particle moves in a straight line for $t<0$ and on a parabolic path for $t>0$? If not, suggest a suitable physical context for this graph.

---

Answer

No, this interpretation is NOT correct.

The statement is incorrect because the given figure is an x–t (position–time) graph, not a path diagram.

Correct Explanation

• The graph shows how position x

  of the particle changes with time t

• It does not represent the actual path in space.

• Therefore:

  • A straight line in an x–t graph does not mean straight-line motion in space.

  • A parabolic curve in an x–t graph does not mean a parabolic path.

In fact, the motion is one-dimensional throughout, i.e., the particle always moves along the same straight line (x-axis) for all values of time.

---

Question 2.14 

A police van moving on a highway with a speed of 30 km h⁻¹ fires a bullet at a thief’s car speeding away in the same direction with a speed of 192 km h⁻¹. If the muzzle speed of the bullet is 150 m s⁻¹, with what speed does the bullet hit the thief’s car?

(Relevant speed is the speed of the bullet relative to the car.)

---

Step 1: Convert all speeds into SI units

Police van speed

$$30{\text{km h}}^{-1}=\frac{30\times 1000}{3600}=8.33{\text{m s}}^{-1}$$

Thief’s car speed

$$192{\text{km h}}^{-1}=\frac{192\times 1000}{3600}=53.33{\text{m s}}^{-1}$$

 

Step 2: Speed of bullet relative to ground

The bullet is fired from the moving police van, so its speed relative to the ground is:

$$v_{\text{bullet, ground}}=150+8.33=158.33{\text{m s}}^{-1}$$

Step 3: Speed of bullet relative to thief’s car

This is the speed that causes damage.

$$v_{\text{relative}}=v_{\text{bullet}}-v_{\text{car}}$$

$$v_{\text{relative}}=158.33-53.33=105{\text{m s}}^{-1}$$

---

Question 2.15

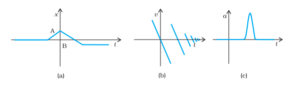
Suggest a suitable physical situation for each of the graphs shown in Fig. 2.12.

Graph-wise Analysis

Graph (a): x–t graph (Position–Time) ✅ Possible

• The particle moves forward, reaches a maximum position, and then moves backward.

• At every instant of time, there is only one position.

• The sharp corner only indicates a sudden change in velocity, which is allowed in an idealised graph.

✔️ This CAN represent one-dimensional motion.

---

Graph (b): v–t graph (Velocity–Time) ❌ Not Possible

• At the same instant of time, the graph shows more than one velocity (multiple slanted lines overlapping the same time).

• In one-dimensional motion, a particle can have only one velocity at a given instant.

❌ This CANNOT represent one-dimensional motion.

---

Graph (c): a–t graph (Acceleration–Time) ✅ Possible

• Acceleration is zero most of the time and becomes non-zero for a short interval.

• This can happen when a force acts briefly, such as:

  • a bat hitting a ball,

  • a hammer striking a nail.

✔️ This CAN represent one-dimensional motion.

---

Question 2.16 

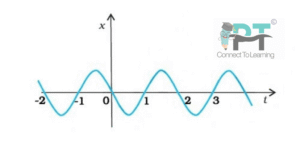
Figure 2.13 gives the x–t plot of a particle executing one-dimensional simple harmonic motion.
(You will learn about this motion in more detail in Chapter 13).

Give the signs of position, velocity and acceleration variables of the particle at

$$t=0.3\text{ s},1.2\text{ s},-1.2\text{ s}\mathrm{.}$$

Answer

From the given x–t graph of SHM:

• Position (x): sign depends on whether the curve is above (+) or below (–) the time axis.

• Velocity (v): sign depends on the slope of the x–t graph

  • rising → v positive

  • falling → v negative

• Acceleration (a) in SHM:

  $$a=-{\omega }^{2}x$$

  so acceleration is always opposite in sign to displacement.

---

At $t=0.3\text{s}$

• Position: negative (below x-axis)

• Velocity: negative (curve falling)

• Acceleration: positive (opposite to x)

$$\boxed{{\displaystyle x<0,v<0,a>0}}$$

---

At $t=1.2\text{s}$

• Position: positive (above x-axis)

• Velocity: negative (curve falling)

• Acceleration: negative

$$\boxed{{\displaystyle x>0,v<0,a<0}}$$

---

At $t=-1.2\text{s}$

• Position: positive

• Velocity: positive (curve rising)

• Acceleration: negative

$$\boxed{{\displaystyle x>0,v>0,a<0}}$$

Final Summary Table

---

Question 2.17 

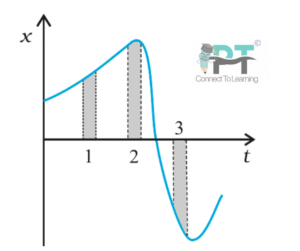
Figure 2.14 gives the x–t plot of a particle in one-dimensional motion. Three different equal intervals of time are shown.

(a) In which interval is the average speed greatest, and in which is it the least?
(b) Give the sign of average velocity for each interval.

Answer

Key ideas to use:

• Average speed = total distance covered ÷ time
  → depends on how steep the x–t graph is (ignores direction).

• Average velocity = displacement ÷ time
  → sign depends on whether x increases (+) or decreases (–) with time.

(a) Average speed

From the graph (equal time intervals):

• Greatest average speed → Interval II
  (the graph is steepest → maximum distance covered in the same time)

• Least average speed → Interval I
  (the graph is least steep → minimum distance covered)

---

(b) Sign of average velocity

• Interval I: position increases with time
  → average velocity is positive (+)

• Interval II: position still increases with time
  → average velocity is positive (+)

• Interval III: position decreases with time
  → average velocity is negative (–)

---

Question 2.18 

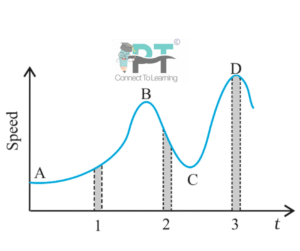
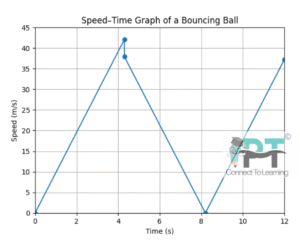
Figure 2.15 gives a speed–time graph of a particle in motion along a constant direction.
Three equal intervals of time are shown.

(a) In which interval is the average acceleration greatest in magnitude?
(b) In which interval is the average speed greatest?
(c) Choosing the positive direction as the constant direction of motion, give the signs of velocity (v) and acceleration (a) in the three intervals.
(d) What are the accelerations at the points A, B, C and D?

Answer

Key ideas from a speed–time (v–t) graph

• Average acceleration = slope of the v–t graph over an interval

• Average speed = average value of speed in that interval

• Instantaneous acceleration at a point = slope of the tangent at that point

• Motion is along a constant positive direction, so v is always positive

---

(a) Interval with greatest average acceleration (magnitude)

• The steepest change of speed occurs in Interval I

$$\boxed{{\displaystyle \text{Greatest average acceleration (magnitude): Interval I}}}$$

---

(b) Interval with greatest average speed

• The highest speeds overall are in Interval III

$$\boxed{{\displaystyle \text{Greatest average speed: Interval III}}}$$

---

(c) Signs of velocity and acceleration

Since the particle always moves in the chosen positive direction:

---

(d) Accelerations at points A, B, C and D

Acceleration at a point = slope of the v–t curve at that point.

 

 

 

 

From Question 2.1 to 2.9

Question 2.1
In which of the following examples of motion, can the body be considered approximately a point object?
(a) a railway carriage moving without jerks between two stations.
(b) a monkey sitting on top of a man cycling smoothly on a circular track.
(c) a spinning cricket ball that turns sharply on hitting the ground.
(d) a tumbling beaker that has slipped off the edge of a table.

Answer:

A body can be treated as a point object when:

• its size is negligible compared to the distance travelled, and
• rotation or shape does not affect the description of motion.

(a) Railway carriage ✔
The distance between stations is very large compared to the size of the carriage. Its size does not affect the motion.

Can be treated as a point object.

(b) Monkey on a man cycling ✔
The motion of the system (man + monkey) is smooth and its size is small compared to the circular track.

Can be treated as a point object.

(c) Spinning cricket ball ✘
The spinning and turning of the ball are important. Size and rotation cannot be ignored.

Cannot be treated as a point object.

(d) Tumbling beaker ✘
The beaker rotates and changes orientation while falling. Its shape matters.
Cannot be treated as a point object.

Correct answer: (a) and (b)

---

Question 2.2
The position–time (x–t) graphs for two children A and B returning from their school O to their homes P and Q respectively are shown. Choose the correct entries in the brackets below:
(a) (A/B) lives closer to the school than (B/A)
(b) (A/B) starts from the school earlier than (B/A)
(c) (A/B) walks faster than (B/A)
(d) A and B reach home at the (same/different) time
(e) (A/B) overtakes (B/A) on the road (once/twice)

Answer:

Important ideas used:

• Distance from school → final position on x-axis
• Who starts earlier → whose graph begins earlier on time axis
• Speed → slope of x–t graph
• Overtaking → point where two graphs intersect

---

(a) A lives closer to the school than B
A’s final position is less than B’s.
 A lives closer.

(b) B starts earlier than A
B’s graph begins at an earlier time.
 B starts earlier.

(c) A walks faster than B
Slope of A’s graph is steeper than that of B.
 A walks faster.

(d) A and B reach home at the same time
Both graphs end at the same time on the time axis.
 Same time.

(e) A overtakes B once
The two graphs intersect at one point.
 A overtakes B once.

---

Question 2.3
A woman starts from her home at 9.00 am, walks with a speed of 5 km h⁻¹ on a straight road up to her office 2.5 km away, stays at the office up to 5.00 pm, and returns home by an auto with a speed of 25 km h⁻¹. Choose suitable scales and plot the x–t graph of her motion.

---

Step 1: Choose origin and directions

• Take home as origin (x = 0).
• Direction from home to office is taken as positive x-direction.
• Motion is one-dimensional along a straight road.

---

Step 2: Motion from home to office

• Distance = 2.5 km
• Speed = 5 km h⁻¹

$$\text{Time taken}=\frac{2.5}{5}=0.5\text{ h}=30\text{ minutes}$$

She starts at 9:00 am, so she reaches office at 9:30 am.

This part of motion is uniform motion, so x–t graph is a straight line with positive slope.

---

Step 3: Stay at office

• She stays from 9:30 am to 5:00 pm.
• Position remains constant at x = 2.5 km.
• Duration of rest = 7.5 hours.

On x–t graph, this is shown by a horizontal straight line.

---

Step 4: Return journey (office to home)

• Speed of auto = 25 km h⁻¹
• Distance = 2.5 km

$$\text{Time taken}=\frac{2.5}{25}=0.1\text{ h}=6\text{ minutes}$$

She starts at 5:00 pm and reaches home at 5:06 pm.

Since she is moving towards home, displacement decreases.
 The x–t graph is a straight line with negative slope, steeper than the walking line.

---

Step 5: Summary of key points for the graph

Step 6: Choosing suitable scales

You may choose, for example:

• Time axis (t-axis):
  1 cm = 1 hour
• Position axis (x-axis):
  1 cm = 0.5 km

(Any other convenient and proportional scale is acceptable.)

---

Step 7: Shape of the x–t graph

1. Straight rising line from (9:00 am, 0) to (9:30 am, 2.5 km)
2. Horizontal line from 9:30 am to 5:00 pm at x = 2.5 km
3. Steep straight falling line from (5:00 pm, 2.5 km) to (5:06 pm, 0)

---

Question 2.4
A drunkard walking in a narrow lane takes 5 steps forward and 3 steps backward, followed again by 5 steps forward and 3 steps backward, and so on. Each step is 1 m long and requires 1 s. Plot the x–t graph of his motion. Determine graphically and otherwise how long the drunkard takes to fall in a pit 13 m away from the start.

---

Step 1: Understand the motion

• Length of each step = 1 m
• Time for each step = 1 s

One complete cycle:

• Forward steps = 5 m in 5 s
• Backward steps = 3 m in 3 s

Net displacement in one cycle

$$=5-3=2\text{ m}$$

Time for one cycle

$$=5+3=8\text{ s}$$

---

Step 2: Motion in successive cycles

After 6 cycles, the drunkard reaches 12 m.

---

Step 3: Final motion to the pit

The pit is at 13 m from the start.

At the end of 6 cycles:

• Position = 12 m
• Time = 48 s

Now the drunkard moves forward:

• 1 forward step = 1 m in 1 s

So, to go from 12 m to 13 m:

$$\text{Time required}=1\text{ s}$$

---

Step 4: Total time (by calculation)

$$\text{Total time}=48+1=\boxed{{\displaystyle 49\text{ s}}}$$

---

Step 5: x–t graph description (graphical method)

How to draw the x–t graph:

• x-axis → time (s)
• y-axis → position (m)

Nature of graph:

• Slanted rising straight lines → forward motion
• Slanted falling straight lines → backward motion
• Repeated zig-zag pattern
• The graph finally reaches x = 13 m at t = 49 s

From the graph, the point where the line first touches x = 13 m gives the same result:

$$\boxed{{\displaystyle t=49\text{ s}}}$$

---

Question 2.5
A car moving along a straight highway with speed of 126 km h⁻¹ is brought to a stop within a distance of 200 m. What is the retardation of the car (assumed uniform), and how long does it take for the car to stop?

---

Step 1: Write the given data

• Initial speed,$$u=126{\text{ km h}}^{-1}=\frac{126\times 1000}{3600}=35{\text{ m s}}^{-1}$$
  
• Final speed,$$v=0{\text{ m s}}^{-1}(\text{car comes to rest})$$
• Distance covered before stopping,$$s=200\text{ m}$$

---

Step 2: Find the retardation

Use the equation of motion:

$$v^2=u^2+2as$$

Substitute the values:

$$0=(35{)}^2+2a(200)$$
$$0=1225+400a$$
$$a=-\frac{1225}{400}=-3.06{\text{ m s}}^{-2}$$

Retardation

$$\boxed{{\displaystyle 3.06{\text{ m s}}^{-2}}}$$

(Negative sign indicates deceleration or retardation.)

---

Step 3: Find the time taken to stop

Use the equation:

$$v=u+at$$
$$0=35+(-3.06)t$$
$$t=\frac{35}{3.06}\approx 11.4\text{ s}$$

---

---

Question 2.6
A player throws a ball upwards with an initial speed of 29.4 m s⁻¹.

(a) What is the direction of acceleration during the upward motion of the ball?
(b) What are the velocity and acceleration of the ball at the highest point of its motion?
(c) Choose x = 0 m and t = 0 s to be the location and time of the ball at its highest point, vertically downward direction to be the positive direction of x-axis, and give the signs of position, velocity and acceleration of the ball during its upward and downward motion.
(d) To what height does the ball rise and after how long does the ball return to the player’s hands?
(Take g = 9.8 m s⁻² and neglect air resistance.)

---

(a) Direction of acceleration during upward motion

The acceleration of the ball is due to gravity, which always acts vertically downward, irrespective of the direction of motion.

Answer:

The acceleration during upward motion is vertically downward.

---

(b) Velocity and acceleration at the highest point

At the highest point:

• The ball momentarily comes to rest, so velocity is zero.
• Gravity still acts downward, so acceleration is not zero.

Answer:

• Velocity = 0
• Acceleration = 9.8 m s⁻² downward

---

(c) Signs of position, velocity and acceleration

Given sign convention:

• Highest point → x = 0 m
• Time at highest point → t = 0 s
• Downward direction is positive

---

Upward motion (before reaching highest point)

• Position: Below the highest point → negative
• Velocity: Moving upward (opposite to positive direction) → negative
• Acceleration: Gravity acts downward → positive

---

Downward motion (after highest point)

• Position: Below the highest point → positive
• Velocity: Moving downward → positive
• Acceleration: Gravity acts downward → positive

---

(d) Maximum height and time of flight

Given:

• Initial speed,$$u=29.4{\text{ m s}}^{-1}$$
• Acceleration due to gravity,$$a=-9.8{\text{ m s}}^{-2}$$
• Velocity at highest point,$$v=0$$

---

Maximum height reached

Use:

$$v^2=u^2+2as$$
$$0=(29.4{)}^2+2(-9.8)h$$
$$0=864.36-19.6h$$
$$h=\frac{864.36}{19.6}=44.1\text{ m}$$

---

Time to reach highest point

Use:

$$v=u+at$$
$$0=29.4-9.8t$$
$$t=3\text{ s}$$

---

Total time to return to player

Time of ascent = Time of descent

$$\text{Total time}=2\times 3=\boxed{{\displaystyle 6\text{ s}}}$$

---

Question 2.7
Read each statement below carefully and state with reasons and examples, if it is true or false. A particle in one-dimensional motion:

---

(a) with zero speed at an instant may have non-zero acceleration at that instant

Answer: True

Reason:
Speed can be zero at an instant while acceleration is non-zero if the velocity is changing at that instant.

Example:
A ball thrown vertically upward has zero speed at the highest point, but its acceleration due to gravity is 9.8 m s⁻² downward.

---

(b) with zero speed may have non-zero velocity

Answer: False

Reason:
Velocity is a vector quantity whose magnitude is speed.
If speed is zero, the magnitude of velocity is zero, hence velocity must also be zero.

Example:
An object at rest has zero speed and zero velocity.

---

(c) with constant speed must have zero acceleration

Answer: False

Reason:
Acceleration depends on change in velocity. Velocity can change due to change in direction even if speed remains constant.

Example:
Uniform circular motion has constant speed, but acceleration is present because direction of velocity changes continuously.

(Note: In one-dimensional straight-line motion, constant speed implies zero acceleration.)

---

(d) with positive value of acceleration must be speeding up

Answer: False

Reason:
Whether a particle speeds up or slows down depends on the relative directions of velocity and acceleration, not just the sign of acceleration.

Example:
A ball thrown vertically upward has positive acceleration downward, but its speed decreases during upward motion.

---

Question 2.8

A ball is dropped from a height of 90 m on a floor. At each collision with the floor, the ball loses one-tenth of its speed. Plot the speed–time graph of its motion between t = 0 to 12 s.

---

Given

• Height, $h=90\text{m}$

• Initial velocity, $u=0$

• Acceleration due to gravity, $g=9.8{\text{m s}}^{-2}$

• At each collision, speed reduces to $\frac{9}{10}$ of its value just before impact.

• 

---

Step 1: First fall (0 to first impact)

Using

$$h=\frac{1}{2}g{t}^2$$

$$90=\frac{1}{2}\times 9.8\times t^2$$

$$t^2=\frac{180}{9.8}\approx 18.37$$

$$t_1\approx 4.3\text{s}$$

Speed just before hitting the floor:

$$v_1=g{t}_1=9.8\times 4.3\approx 42.1{\text{m s}}^{-1}$$

---

Step 2: Speed just after first collision

Loss of one-tenth speed:

$$v_1^{\mathrm{\prime }}=\frac{9}{10}\times 42.1\approx 37.9{\text{m s}}^{-1}$$

This is upward speed immediately after collision.

---

Step 3: Motion after first bounce

• The ball moves upward, speed decreases uniformly to zero.

• Time to reach maximum height:

$$t_{\text{up}}=\frac{v_1^{\mathrm{\prime }}}{g}=\frac{37.9}{9.8}\approx 3.9\text{s}$$

• Total time till top of first bounce:

$$4.3+3.9=8.2\text{s}$$

Speed becomes zero at this point.

---

Step 4: Second fall (within 12 s)

• From 8.2 s onward, the ball starts falling again.

• Speed increases linearly from 0.

• Time available:

$$12-8.2=3.8\text{s}$$

Speed at $t=12\text{s}$:

$$v=gt=9.8\times 3.8\approx 37.2{\text{m s}}^{-1}$$

(No second collision occurs within 12 s.)

 Speed–Time Graph (Description)
0 to 4.3 s → Straight line rising from 0 to 42.1 m/s
Sudden drop at 4.3 s to 37.9 m/s (collision)
4.3 to 8.2 s → Straight line falling to zero (upward motion)
8.2 to 12 s → Straight line rising again (downward motion)
⚠️ Important NCERT Point:
Speed–time graph has sharp vertical drops at collision points because speed changes suddenly.

---

Question 2.9

Explain clearly, with examples, the distinction between:
(a) Magnitude of displacement and total path length
(b) Magnitude of average velocity and average speed

Show that in both cases the second quantity is greater than or equal to the first.
When does equality hold?
(Consider one-dimensional motion only.)

---

(a) Displacement (magnitude) vs Total Path Length

Displacement

• Displacement is the shortest straight-line distance between the initial and final positions of a particle.

• It depends only on the initial and final positions, not on the actual path followed.

• It can be positive, negative or zero.

• Its magnitude is always less than or equal to the path length.

Total Path Length (Distance)

• Total path length is the actual length of the path travelled by the particle.

• It depends on the entire motion.

• It is always positive.

• It is always greater than or equal to the magnitude of displacement.

Example

Suppose a particle moves:

• From $x=0$ m to $x=10$,

• Then back to $x=4$.

• Magnitude of displacement

  $$=\mathrm{\mid }4-0\mathrm{\mid }=4\text{m}$$

• Total path length

  $$=10+6=16\text{m}$$

$$\text{Path length}>\text{Magnitude of displacement}$$

Equality condition

• Equality holds only when the particle moves in a straight line without changing direction.

---

(b) Magnitude of Average Velocity vs Average Speed

Average Velocity

• Average velocity is defined as:

$$\text{Average velocity}=\frac{\text{Displacement}}{\text{Time interval}}$$

• Its magnitude depends only on displacement.

• It can be zero, even if the particle has moved.

Average Speed

• Average speed is defined as:

$$\text{Average speed}=\frac{\text{Total path length}}{\text{Time interval}}$$

• It depends on the entire distance travelled.

• It is always positive.

---

Why average speed ≥ magnitude of average velocity

Since:

$$\text{Total path length}\ge \text{Magnitude of displacement}$$

Dividing both sides by time:

$$\text{Average speed}\ge \text{Magnitude of average velocity}$$

---

Example

A person walks:

• 10 m forward in 10 s,

• then 10 m backward in 10 s.

• Displacement = 0

• Total path length = 20 m

• Time = 20 s

$$\text{Magnitude of average velocity}=\frac{0}{20}=0$$$$\text{Average speed}=\frac{20}{20}=1{\text{m s}}^{-1}$$

$$\text{Average speed}>\text{Magnitude of average velocity}$$

---

Equality condition

• Equality holds only when motion is along a straight line without reversal of direction.

---

Final Conclusion (Very Important for Exams)

Equality holds only for straight-line motion in one direction.