Tag: Miscellaneous Exercise on Chapter 6 Question 5 NCERT Maths Class 12th Solution

Question 5

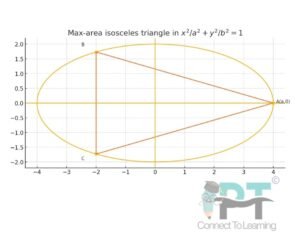
Find the maximum area of an isosceles triangle inscribed in the ellipse

$$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$

with its vertex at one end of the major axis.

Solution

Assume $a>b$, so the major axis is along the $x$-axis.
Take the vertex of the isosceles triangle at the right end of the major axis:

$$A(a,0)\mathrm{.}$$

Let the other two vertices be symmetric about the $x$-axis (this gives an isosceles triangle and will turn out to be the max–area case):

$$B(a\cos \theta ,b\sin \theta ),C(a\cos \theta ,-b\sin \theta ),0<\theta <\pi \mathrm{.}$$

These lie on the ellipse since they are in parametric form:

$$x=a\cos \theta ,y=\pm b\sin \theta \mathrm{.}$$

Area of the triangle

• Base $BC$ is vertical:

  $$\text{length of }BC=2b\sin \theta \mathrm{.}$$

• Height is the horizontal distance from $A(a,0)$ to the line $x=a\cos \theta$:

  $$\text{height}=a-a\cos \theta =a(1-\cos \theta )\mathrm{.}$$

So the area $A(\theta )$ of triangle $ABC$ is

$$A(\theta )=\frac{1}{2}\times \text{base}\times \text{height}=\frac{1}{2}\cdot 2b\sin \theta \cdot a(1-\cos \theta )=ab\sin \theta (1-\cos \theta )\mathrm{.}$$

We must maximize

$$A(\theta )=ab\sin \theta (1-\cos \theta ),0<\theta <\pi \mathrm{.}$$

Maximize $A(\theta )$

Differentiate:

$$A(\theta )=ab(\sin \theta -\sin \theta \cos \theta ),$$
$$A^{\mathrm{\prime }}(\theta )=ab(\cos \theta -({\cos }^2\theta -{\sin }^2\theta ))\mathrm{.}$$

Use ${\sin }^2\theta =1-{\cos }^2\theta$:

$${\cos }^2\theta -{\sin }^2\theta ={\cos }^2\theta -(1-{\cos }^2\theta )=2{\cos }^2\theta -1.$$

So

$$A^{\mathrm{\prime }}(\theta )=ab(\cos \theta -(2{\cos }^2\theta -1))=ab(1+\cos \theta -2{\cos }^2\theta )\mathrm{.}$$

Set $A^{\mathrm{\prime }}(\theta )=0$:

$$1+\cos \theta -2{\cos }^2\theta =0.$$

Let $c=\cos \theta$. Then

$$2c^2-c-1=0$$
$$\Rightarrow c=\frac{1\pm \sqrt{1+8}}{4}=\frac{1\pm 3}{4}=1,-\frac{1}{2}\mathrm{.}$$

• $\cos \theta =1\Rightarrow \theta =0$, which gives zero area, so not a maximum.

• $\cos \theta =-\frac{1}{2}\Rightarrow \theta =\frac{2\pi }{3}$in $(0,\pi )$, valid.

Then

$$\sin \theta =\sin \frac{2\pi }{3}=\frac{\sqrt{3}}{2}\mathrm{.}$$

Substitute in the area:

$$A_{\max }=ab\sin \theta (1-\cos \theta )=ab\left(\frac{\sqrt{3}}{2}\right)(1-(-\frac{1}{2}))=ab\left(\frac{\sqrt{3}}{2}\right)\left(\frac{3}{2}\right)=\frac{3\sqrt{3}}{4}ab\mathrm{.}$$

Final Answer

$$\boxed{{\displaystyle \text{The maximum area of the isosceles triangle is }\frac{3\sqrt{3}}{4}ab\mathrm{.}}}$$