Tag: NCERT 12th maths-miscellaneous exercise on chapter-6 question-4 solution

Question 4

Find the intervals in which the function

$$f(x)=x^3+\frac{1}{x^3},x\mathrm{\ne }0$$

is (i) increasing (ii) decreasing.

Solution

Step 1: Differentiate the function

$$f(x)=x^3+x^{-3}$$
$$f^{\mathrm{\prime }}(x)=3x^2-3x^{-4}$$
$$f^{\mathrm{\prime }}(x)=3(x^2-\frac{1}{x^4})$$
$$f^{\mathrm{\prime }}(x)=3\cdot \frac{x^6-1}{x^4}$$
$$f^{\mathrm{\prime }}(x)=\frac{3(x^6-1)}{x^4}$$

Step 2: Determine where $f^{\mathrm{\prime }}(x)>0$ or $f^{\mathrm{\prime }}(x)<0$

The denominator $x^4>0$ for all $x\mathrm{\ne }0$, so the sign of $f^{\mathrm{\prime }}(x)$ depends on the numerator:

$$x^6-1$$

Solve:

$$x^6-1>0\Rightarrow x^6>1\Rightarrow \mathrm{\mid }x\mathrm{\mid }>1$$
$$x^6-1<0\Rightarrow x^6<1\Rightarrow \mathrm{\mid }x\mathrm{\mid }<1,x\mathrm{\ne }0$$

Final Result

(i) Increasing intervals

$$f^{\mathrm{\prime }}(x)>0\Rightarrow \mathrm{\mid }x\mathrm{\mid }>1$$
$$\boxed{{\displaystyle \text{The function is increasing in }(-\mathrm{\infty },-1)\cup (1,\mathrm{\infty })}}$$

(ii) Decreasing intervals

$$f^{\mathrm{\prime }}(x)<0\Rightarrow 0<\mathrm{\mid }x\mathrm{\mid }<1$$
$$\boxed{{\displaystyle \text{The function is decreasing in }(-1,0)\cup (0,1)}}$$

Summary

$$\begin{gathered} \boxed{{\displaystyle \text{Increasing : }(-\mathrm{\infty },-1)\cup (1,\mathrm{\infty }) \\ \text{Decreasing : }(-1,0)\cup (0,1)}} \end{gathered}$$

---

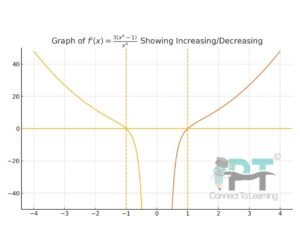
Let’s check the graph of the given function :

Following is the graph of the derivative of the function: