Class 11th Physics Chapter-5 Solutions

Go back to CLASS 11th Physics Page

Question 5.1

The sign of work done by a force on a body is important to understand. State carefully whether the following quantities are positive or negative:

Answer: 

(a) Work done by a man in lifting a bucket

Positive
The force applied by the man is in the same direction as the displacement of the bucket (upward), so the work done is positive.

---

(b) Work done by gravitational force

Negative
Gravity acts downward while the bucket moves upward. Since force and displacement are in opposite directions, the work done by gravity is negative.

---

(c) Work done by friction on a body sliding down an inclined plane

Negative
Friction always acts opposite to the direction of motion. As the body slides down, friction acts upward along the plane, so its work is negative.

---

(d) Work done by an applied force on a body moving on a rough horizontal plane with uniform velocity

Positive
The applied force acts in the direction of motion to balance friction. Hence, the work done by the applied force is positive
(while friction does equal negative work).

---

(e) Work done by the resistive force of air on a vibrating pendulum

Negative
Air resistance opposes the motion of the pendulum and removes energy from it, bringing it to rest. Therefore, the work done by air resistance is negative.

---

Question 5.2

A body of mass 2 kg, initially at rest, moves under the action of an applied horizontal force of 7 N on a table. The coefficient of kinetic friction between the body and the table is 0.1.

Compute:
(a) work done by the applied force in 10 s,
(b) work done by friction in 10 s,
(c) work done by the net force on the body in 10 s,
(d) change in kinetic energy of the body in 10 s,

and interpret the results.

---

Solution

Given:

$$m=2\text{ kg},F=7\text{ N},{\mu }_k=0.1,t=10\text{ s}$$

Take$$g=10{\text{ m s}}^{-2}$$

---

Step 1: Forces acting on the body

Normal reaction:

$$N=mg=2\times 10=20\text{ N}$$

Frictional force:

$$f_k={\mu }_{k}N=0.1\times 20=2\text{ N}$$

Net force:

$$F_{\text{net}}=7-2=5\text{ N}$$

---

Step 2: Acceleration of the body

$$a=\frac{F_{\text{net}}}{m}=\frac{5}{2}=2.5{\text{ m s}}^{-2}$$

---

Step 3: Displacement in 10 s

Initial velocity $u=0$

$$s=ut+\frac{1}{2}a{t}^2$$

$$s=0+\frac{1}{2}\times 2.5\times (10{)}^2$$

$$s=125\text{ m}$$

(a) Work done by the applied force

$$W_{\text{applied}}=F\times s=7\times 125$$

$$\boxed{{\displaystyle W_{\text{applied}}=875\text{ J}}}$$

---

(b) Work done by friction

Friction acts opposite to motion:

$$W_{\text{friction}}=-f_k\times s=-2\times 125$$

$$\boxed{{\displaystyle W_{\text{friction}}=-250\text{ J}}}$$

---

(c) Work done by the net force

$$W_{\text{net}}=F_{\text{net}}\times s=5\times 125$$

$$\boxed{{\displaystyle W_{\text{net}}=625\text{ J}}}$$

---

(d) Change in kinetic energy

Final velocity:

$$v=u+at=0+2.5\times 10=25{\text{ m s}}^{-1}$$

Initial kinetic energy:

$$K_i=0$$

Final kinetic energy:

$$K_f=\frac{1}{2}m{v}^2=\frac{1}{2}\times 2\times {25}^2=625\text{ J}$$

$$\boxed{{\displaystyle \mathrm{\Delta }K=625\text{ J}}}$$

---

Question 5.3

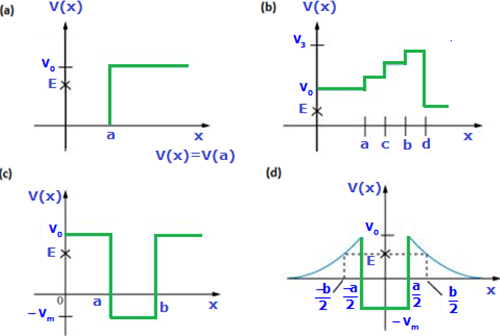
Given in Fig. 5.11 are examples of some potential energy functions in one dimension. The total energy of the particleis indicated by a cross on the ordinate axis.

In each case, specify the regions, if any, in which the particle cannot be found for the given energy. Also, indicate the minimum total energy the particle must have in each case. Think of simple physical contexts for which these potential energy shapes are relevant.

Answer:

For a particle moving in one dimension, the total energy $E$ is the sum of kinetic and potential energies:

$$E=K+V(x)$$

Since kinetic energy $K\ge 0$, the particle can exist only in regions where

$$E\ge V(x)$$

Regions where $V(x)>E$ are classically forbidden.

---

Case (a): Constant potential energy

Regions where the particle cannot be found:

• None, provided $E$ is greater than or equal to the constant value of $V$.

Minimum total energy:

$$E_{\min }=V$$

Physical context:

• A free particle moving on a smooth horizontal surface.

• An idealised electron moving freely inside a metal.

---

Case (b): Potential well (minimum in the middle)

Regions where the particle cannot be found:

• Regions on either side of the well where

$$V(x)>E$$

• The particle is confined between two turning points where $E=V(x)$.

Minimum total energy:

$$E_{\min }=V_{\min }$$

(the lowest value of the potential energy)

Physical context:

• A ball in a valley.

• A mass–spring system oscillating about equilibrium.

• Vibrational motion of atoms in a molecule.

---

Case (c): Potential barrier or step potential

Regions where the particle cannot be found:

• If $E<V_0$, the region beyond the barrier (where $V=V_0$) is forbidden.

• If $E\ge V_0$, there is no forbidden region.

Minimum total energy:

$$E_{\min }=\text{lowest value of }V(x)$$

Physical context:

• A particle approaching a wall or step.

• A classical analogue of a particle facing a potential barrier.

---

Question 5.4

The potential energy function for a particle executing linear simple harmonic motion is given by

$$V(x)=\frac{1}{2}k{x}^2,$$ where $k$ is the force constant of the oscillator. For

$$k=0.5{\text{ N m}}^{-1},$$

the graph of $V(x)$ versus $x$ is shown in Fig. 5.12. Show that a particle of total energy 1 J moving under this potential must turn back when it reaches

$$x=\pm 2\text{ m}\mathrm{.}$$

---

Solution

For motion in one dimension, the total energy $E$ of the particle is

$$E=K+V(x),$$

where $K$ is kinetic energy and $V(x)$ is potential energy.

Since kinetic energy cannot be negative,

$$K\ge 0\Rightarrow E\ge V(x)\mathrm{.}$$

---

Step 1: Write the potential energy function

Given:

$$V(x)=\frac{1}{2}k{x}^2$$

Substitute $k=0.5{\text{N m}}^{-1}$:

$$V(x)=\frac{1}{2}\times 0.5x^2=0.25x^2$$

---

Step 2: Find the turning points

At the turning points, the particle momentarily comes to rest, so

$$K=0\Rightarrow E=V(x)$$

Given total energy:

$$E=1\text{ J}$$

So,

$$0.25x^2=1$$

$$x^2=4$$

$$x=\pm 2\text{ m}$$

---

Question 5.5

Answer the following:

(a)

The casing of a rocket in flight burns up due to friction. At whose expense is the heat energy required for burning obtained — the rocket or the atmosphere?

Answer:
The heat energy required for burning is obtained at the expense of the rocket’s kinetic energy.
Due to air friction, part of the rocket’s mechanical energy is converted into heat. The atmosphere only acts as a medium; it does not supply energy.

---

(b)

Comets move around the sun in highly elliptical orbits. The gravitational force on the comet due to the sun is not normal to the comet’s velocity in general. Yet the work done by the gravitational force over every complete orbit of the comet is zero. Why?

Answer:
Gravitational force is a conservative force.
For conservative forces, the work done over a closed path is zero, irrespective of the shape of the path.
Since a complete orbit is a closed path, the total work done by gravity on the comet over one revolution is zero.

---

(c)

An artificial satellite orbiting the earth in a very thin atmosphere loses its energy gradually due to atmospheric resistance. Why then does its speed increase as it comes closer and closer to the earth?

Answer:
As the satellite loses energy, it moves to a lower orbit, closer to the earth.
In a lower orbit, the gravitational pull is stronger, and the satellite must move with a higher speed to remain in orbit.
Thus, although the total mechanical energy decreases, the kinetic energy (and speed) increases as the satellite approaches the earth.

(d)

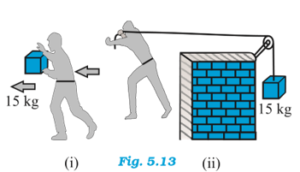
In Fig. 5.13(i), a man walks 2 m carrying a mass of 15 kg in his hands. In Fig. 5.13(ii), he walks the same distance pulling a rope over a pulley with a 15 kg mass hanging at the other end. In which case is the work done greater?

Answer:

• Case (i): Carrying the mass
  The force applied by the man on the mass is vertical, while the displacement is horizontal.
  Since force and displacement are perpendicular,

  $$W=Fd\cos {90}^{\circ }=0$$

  Hence, no work is done on the mass.

• Case (ii): Pulling the rope
  The applied force causes the hanging mass to move upward.
  Force and displacement are in the same direction, so positive work is done.

$$\boxed{{\displaystyle \text{More work is done in case (ii).}}}$$

---

Question 5.6

Underline the correct alternative:

---

(a) When a conservative force does positive work on a body, the potential energy of the body
increases / decreases / remains unaltered

✔ Correct: decreases
(Because $\mathrm{\Delta }V=-W$)

---

(b) Work done by a body against friction always results in a loss of its
kinetic / potential energy

✔ Correct: kinetic
(Friction converts kinetic energy into heat)

---

(c) The rate of change of total momentum of a many-particle system is proportional to the
external force / sum of the internal forces on the system

✔ Correct: external force
(Internal forces cancel in pairs)

---

(d) In an inelastic collision of two bodies, the quantity which does not change after the collision is
total kinetic energy / total linear momentum / total energy of the system of two bodies

✔ Correct: total linear momentum

---

Question 5.7

State whether each of the following statements is true or false. Give reasons for your answer.

---

(a) In an elastic collision of two bodies, the momentum and energy of each body is conserved.

False.
In an elastic collision, the total linear momentum and total kinetic energy of the system are conserved, not those of each individual body. The momentum and kinetic energy of each body generally change due to interaction during the collision.

---

(b) Total energy of a system is always conserved, no matter what internal and external forces on the body are present.

True.
The total energy of the universe is always conserved. Energy may transform from one form to another (mechanical, thermal, chemical, etc.), but it is never destroyed. External forces may change the mechanical energy of a system, but the total energy remains conserved when all forms are included.

---

(c) Work done in the motion of a body over a closed loop is zero for every force in nature.

False.
This is true only for conservative forces (like gravity or spring force).
For non-conservative forces such as friction, the work done over a closed path is not zero.

---

(d) In an inelastic collision, the final kinetic energy is always less than the initial kinetic energy of the system.

True.
In an inelastic collision, part of the initial kinetic energy is converted into other forms of energy such as heat, sound, or deformation. Hence, the final kinetic energy is less than the initial kinetic energy (maximum loss occurs in a perfectly inelastic collision).

---

Question 5.8

Answer carefully, with reasons:

---

(a)

In an elastic collision of two billiard balls, is the total kinetic energy conserved during the short time of collision of the balls (i.e. when they are in contact)?

Answer: No.
During the short time when the two balls are in contact, they are deformed and part of their kinetic energy is temporarily stored as elastic potential energy. Hence, the total kinetic energy is not conserved at every instant during the collision.
However, once the collision is over and the balls separate, the total kinetic energy of the system is restored to its initial value.

---

(b)

Is the total linear momentum conserved during the short time of an elastic collision of two balls?

Answer: Yes.
The forces acting between the two balls during collision are internal forces, which are equal and opposite at every instant (Newton’s third law). Therefore, the total linear momentum of the system remains conserved at all times, including during the collision.

---

(c)

What are the answers to (a) and (b) for an inelastic collision?

• Kinetic energy: Not conserved, even after the collision.
  In an inelastic collision, a part of the initial kinetic energy is permanently converted into other forms of energy such as heat, sound, or energy of deformation.

• Linear momentum: Conserved during the collision.
  As in all collisions, the internal forces between the bodies are equal and opposite at every instant, so the total linear momentum of the system remains conserved (provided external forces are negligible).

---

(d)

If the potential energy of two billiard balls depends only on the separation distance between their centres, is the collision elastic or inelastic?

Answer: The collision is elastic.

Reason:
If the potential energy depends only on the separation between the centres of the balls, the force during collision is a conservative force. For conservative forces, energy stored during deformation is completely recovered when the bodies separate. Hence, no kinetic energy is lost, and the collision is elastic.

---

Question 5.9

A body is initially at rest. It undergoes one-dimensional motion with constant acceleration. The power delivered to it at time $t$ is proportional to:

(i) $t^{1\mathrm{/}2}$
(ii) $t$
(iii) $t^{3\mathrm{/}2}$
(iv) $t^2$

---

Solution

For constant acceleration $a$:

Velocity at time $t$:

$$v=at$$Force on the body:$$F=ma=\text{constant}$$Instantaneous power:

$$P=Fv$$

$$P\propto v\propto t$$

---

Correct answer (5.9):

$$\boxed{{\displaystyle (ii)t}}$$

---

---

Question 5.10

A body is moving unidirectionally under the influence of a source of constant power. Its displacement in time $t$ is proportional to:

(i) $t^{1\mathrm{/}2}$
(ii) $t$
(iii) $t^{3\mathrm{/}2}$
(iv) $t^2$

---

Solution

Power is given by:

$$P=Fv$$

Since power is constant:

$$F\propto \frac{1}{v}$$

Acceleration:$$a=\frac{F}{m}\propto \frac{1}{v}$$

But:

$$a=\frac{dv}{dt}$$

$$\frac{dv}{dt}\propto \frac{1}{v}$$
$$vdv\propto dt$$

Integrating:

$$v^2\propto t\Rightarrow v\propto t^{1\mathrm{/}2}$$

Now, displacement:

$$s=\int vdt\propto \int t^{1\mathrm{/}2}dt$$

$$s\propto t^{3\mathrm{/}2}$$

Correct answer (5.10):

$$\boxed{{\displaystyle (iii)t^{3\mathrm{/}2}}}$$

---

Question 5.11

A body constrained to move along the z-axis of a coordinate system is subject to a constant force

$$\vec{F}=-\widehat{i}+2\widehat{j}+3\widehat{k}\text{ N}$$

where $\widehat{i},\widehat{j},\widehat{k}$ are unit vectors along the x-, y- and z-axes respectively. What is the work done by this force in moving the body a distance of 4 m along the z-axis?

Solution

Displacement vector:

$$\vec{s}=4\widehat{k}\text{ m}$$Work done:

$$W=\vec{F}\cdot \vec{s}=(-\widehat{i}+2\widehat{j}+3\widehat{k})\cdot (4\widehat{k})$$Using dot products:

$$\widehat{i}\cdot \widehat{k}=0,\widehat{j}\cdot \widehat{k}=0,\widehat{k}\cdot \widehat{k}=1$$

$$W=3\times 4=12\text{ J}$$

---

Question 5.12

An electron and a proton are detected in a cosmic ray experiment, the first with kinetic energy 10 keV and the second with 100 keV. Which is faster, the electron or the proton? Obtain the ratio of their speeds.

$$m_e=9.11\times {10}^{-31}\text{ kg},m_p=1.67\times {10}^{-27}\text{ kg},1\text{ eV}=1.60\times {10}^{-19}\text{ J}$$

---

Solution

For non-relativistic speeds, kinetic energy:

$$K=\frac{1}{2}m{v}^2\Rightarrow v=\sqrt{\frac{2K}{m}}$$

---

Convert energies to joules

• Electron:

$$K_e=10\text{ keV}=10\times {10}^3\times 1.60\times {10}^{-19}=1.60\times {10}^{-15}\text{ J}$$

• Proton:

$$K_p=100\text{ keV}=100\times {10}^3\times 1.60\times {10}^{-19}=1.60\times {10}^{-14}\text{ J}$$

Ratio of speeds

$$\frac{v_e}{v_p}=\sqrt{\frac{K_e\mathrm{/}{m}_e}{K_p\mathrm{/}{m}_p}}=\sqrt{\frac{K_e{m}_p}{K_p{m}_e}}$$
$$=\sqrt{\frac{(1.60\times {10}^{-15})(1.67\times {10}^{-27})}{(1.60\times {10}^{-14})(9.11\times {10}^{-31})}}$$Canceling common factors:

$$=\sqrt{0.1\times \frac{1.67\times {10}^{-27}}{9.11\times {10}^{-31}}}=\sqrt{0.1\times 1836}=\sqrt{183.6}$$

$$\boxed{{\displaystyle \frac{v_e}{v_p}\approx 13.5}}$$

---

Question 5.13

A rain drop of radius 2 mm falls from a height of 500 m above the ground. It falls with decreasing acceleration (due to viscous resistance of air) until, at half its original height, it attains its terminal speed, and moves with uniform speed thereafter.

What is the work done by the gravitational force on the drop in the first and second half of its journey?
What is the work done by the resistive force during the entire journey, if its speed on reaching the ground is 10 m s⁻¹?

---

Solution

Given

• Radius of drop:

$$r=2\text{mm}=2\times {10}^{-3}\text{m}$$

• Height fallen:

$$h=500\text{m}$$

• Final speed:

$$v=10{\text{m s}}^{-1}$$

• Density of water:

$$\rho =1000{\text{kg m}}^{-3}$$

• Take

$$g=10{\text{m s}}^{-2}$$

---

Step 1: Mass of the rain drop

Volume of the drop:

$$V=\frac{4}{3}\pi r^3=\frac{4}{3}\pi (2\times {10}^{-3}{)}^3=3.35\times {10}^{-8}{\text{m}}^3$$Mass:

$$m=\rho V=1000\times 3.35\times {10}^{-8}=3.35\times {10}^{-5}\text{kg}$$

---

(a) Work done by gravity

Work done by gravity depends only on vertical displacement, not on speed.

First half (250 m):

$$W_{g1}=mg(250)=3.35\times {10}^{-5}\times 10\times 250$$

$$\boxed{{\displaystyle W_{g1}\approx 0.084\text{ J}}}$$

Second half (250 m):

$$W_{g2}=mg(250)$$

$$\boxed{{\displaystyle W_{g2}\approx 0.084\text{ J}}}$$

---

(b) Work done by resistive force (entire journey)

Total work done by gravity

$$W_g=mg(500)=3.35\times {10}^{-5}\times 10\times 500$$

$$W_g=0.168\text{ J}$$

---

Change in kinetic energy

Initial speed = 0
Final speed = 10 m s⁻¹

$$\mathrm{\Delta }K=\frac{1}{2}m{v}^2=\frac{1}{2}\times 3.35\times {10}^{-5}\times (10{)}^2$$

$$\mathrm{\Delta }K=1.675\times {10}^{-3}\text{ J}$$

Using work–energy theorem

$$\mathrm{\Delta }K=W_g+W_r$$

$$W_r=\mathrm{\Delta }K-W_g$$

$$W_r=(1.675\times {10}^{-3})-0.168$$

$$\boxed{{\displaystyle W_r\approx -0.166\text{ J}}}$$

(The negative sign shows energy loss due to air resistance.)

---

Question 5.14

A molecule in a gas container hits a horizontal wall with speed 200 m s⁻¹ making an angle of 30° with the normal, and rebounds with the same speed. Is momentum conserved in the collision?
Is the collision elastic or inelastic?

---

Answer

Momentum conservation

• The momentum of the molecule alone is not conserved.

• During the collision, the wall exerts a force on the molecule, changing the component of momentum normal to the wall.

• Hence, the molecule’s momentum changes.

However,

• If we consider the combined system of molecule + wall (or Earth), then the total momentum of the system is conserved, because the force between the molecule and the wall is internal to this larger system.

$$\boxed{{\displaystyle \text{Momentum of the molecule alone is not conserved;}}}$$

$$\boxed{{\displaystyle \text{momentum of the system is conserved.}}}$$

Nature of collision (elastic or inelastic)

• The molecule rebounds with the same speed as before collision.

• Hence, its kinetic energy remains unchanged.

• No kinetic energy is lost in the collision.

$$\boxed{{\displaystyle \text{The collision is elastic.}}}$$

---

Question 5.15

A pump on the ground floor of a building can pump up water to fill a tank of volume 30 m³ in 15 min. If the tank is 40 m above the ground, and the efficiency of the pump is 30%, how much electric power is consumed by the pump?

---

Solution

Given

• Volume of water, $V=30{\text{m}}^3$

• Time, $t=15\text{min}=900\text{s}$

• Height, $h=40\text{m}$

• Efficiency, $\eta =30\mathrm{\%}=0.30$

• Density of water, $\rho =1000{\text{kg m}}^{-3}$

• $g=10{\text{m s}}^{-2}$

---

Step 1: Mass of water

$$m=\rho V=1000\times 30=3.0\times {10}^4\text{kg}$$

---

Step 2: Work done in lifting the water

$$W=mgh=3.0\times {10}^4\times 10\times 40$$

$$W=1.2\times {10}^7\text{J}$$

---

Step 3: Useful power output of the pump

$$P_{\text{out}}=\frac{W}{t}=\frac{1.2\times {10}^7}{900}$$

$$P_{\text{out}}\approx 1.33\times {10}^4\text{W}$$

Step 4: Electric power consumed

$$\eta =\frac{P_{\text{out}}}{P_{\text{in}}}\Rightarrow P_{\text{in}}=\frac{P_{\text{out}}}{\eta }$$

$$P_{\text{in}}=\frac{1.33\times {10}^4}{0.30}$$

$$\boxed{{\displaystyle P_{\text{in}}\approx 4.4\times {10}^4\text{W}}}$$

---

Question 5.16

Two identical ball bearings in contact with each other and resting on a frictionless table are hit head-on by another ball bearing of the same mass, moving initially with speed V. If the collision is elastic, which of the following (Fig. 5.14) is a possible result after collision?

---

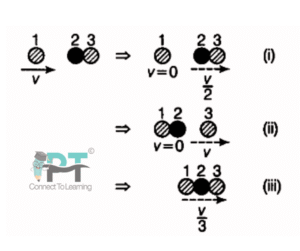
Answer and Explanation

The correct result is the one in which:

• The incoming ball comes to rest,

• The middle ball remains at rest,

• The last ball moves forward with speed V.

---

Reason

All three balls have the same mass, and the collision is elastic. Therefore:

1. Total linear momentum is conserved

2. Total kinetic energy is conserved

This situation is identical to the well-known Newton’s cradle effect.

• Momentum before collision:

$$mV$$

• After collision, for momentum and kinetic energy to be conserved:

  • Only one ball can move with speed $V$,

  • That ball must be the last one,

  • The other two must remain at rest.

Any other outcome (e.g., two balls moving, or all three moving) would violate either momentum conservation or kinetic energy conservation.

Final Answer

$$\boxed{{\displaystyle \text{The incoming ball stops and only the farthest ball moves with speed }V\mathrm{.<span\; style="font-size:\; revert;\; font-family:\; var(--wp--preset--font-family--manrope);\; letter-spacing:\; -0.1px;"></span>}}}$$

 Hence, the figure showing only the last ball moving with speed V is the correct one.

---

Question 5.17

The bob A of a pendulum, released from 30° to the vertical, hits another bob B of the same mass at rest on a table, as shown in Fig. 5.15. How high does bob A rise after the collision? Neglect the size of the bobs and assume the collision to be elastic.

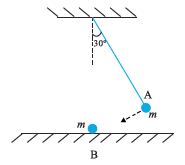
Solution

Step 1: Speed of bob A just before collision

Bob A is released from an angle ${30}^{\circ }$.
Loss in gravitational potential energy = gain in kinetic energy.

If $l$ is the length of the pendulum, the vertical drop is:

$$h=l(1-\cos {30}^{\circ })$$

Using energy conservation:

$$\frac{1}{2}m{v}^2=mgl(1-\cos {30}^{\circ })$$

This gives the speed $v$ of bob A just before collision.

---

Step 2: Nature of collision

• Collision is elastic

• Masses of A and B are equal

• Bob B is initially at rest

• Collision is head-on

For a head-on elastic collision between equal masses:

• The moving body (A) comes to rest

• The stationary body (B) moves off with the same speed

So, immediately after collision:

$$v_A=0$$

---

Step 3: Rise of bob A after collision

Since bob A comes to rest immediately after collision, it has no kinetic energy left to convert into potential energy.

Hence, it does not rise at all.

---

Question 5.18

The bob of a pendulum is released from a horizontal position. If the length of the pendulum is 1.5 m, what is the speed with which the bob arrives at the lowermost point, given that it dissipates 5% of its initial energy against air resistance?

---

Solution

Step 1: Initial potential energy

When released from the horizontal position, the vertical drop of the bob equals the length of the pendulum:

$$h=l=1.5\text{ m}$$

Initial potential energy:

$$E_i=mgh$$Take:

$$g=10{\text{ m s}}^{-2}$$

$$E_i=m\times 10\times 1.5=15m\text{ J}$$

---

Step 2: Energy lost due to air resistance

Given that 5% of initial energy is dissipated:

$$E_{\text{lost}}=0.05\times 15m=0.75m$$

Remaining energy at the lowest point:

$$E_f=15m-0.75m=14.25m$$

---

Step 3: Kinetic energy at the lowest point

At the lowest point, all remaining energy is kinetic:

$$\frac{1}{2}m{v}^2=14.25m$$Cancel $m$:

$$\frac{1}{2}{v}^2=14.25$$

$$v^2=28.5$$

$$v=\sqrt{28.5}\approx 5.34{\text{ m s}}^{-1}$$

---

Question 5.19

A trolley of mass 300 kg carrying a sandbag of mass 25 kg is moving uniformly with a speed of 27 km h⁻¹ on a frictionless track. After a while, sand starts leaking out of a hole on the floor of the trolley at the rate of 0.05 kg s⁻¹.

What is the speed of the trolley after the entire sandbag is empty?

---

Solution

Key physical idea

• The track is frictionless, so there is no external horizontal force on the trolley–sand system.

• The sand leaks vertically downward, so it carries no horizontal momentum relative to the ground.

• Hence, the horizontal momentum of the trolley does not change.

---

Apply conservation of momentum

Initial total mass:

$$M_i=300+25=325\text{ kg}$$

Initial speed:$$u=27{\text{ km h}}^{-1}=7.5{\text{ m s}}^{-1}$$Initial momentum:

$$p_i=325\times 7.5$$

---

After the entire sandbag is empty:

Final mass of trolley:

$$M_f=300\text{ kg}$$Let final speed be $v$.

Since no external horizontal force acts,

$$p_i=p_f$$

$$325\times 7.5=300\times v$$

Solve for $v$

$$v=\frac{325\times 7.5}{300}$$

$$v=8.125{\text{ m s}}^{-1}$$Convert back to km h⁻¹:

$$v=8.125\times 3.6\approx 29.3{\text{ km h}}^{-1}$$

---

Question 5.20

A body of mass 0.5 kg travels in a straight line with velocity

$$v=a{x}^{3\mathrm{/}2},$$where

$$a=5{\text{m}}^{-1\mathrm{/}2}{\text{s}}^{-1}\mathrm{.}$$

What is the work done by the net force during its displacement from

$$x=0\text{ to }x=2\text{ m }?$$

---

Solution

The work done by the net force equals the change in kinetic energy (work–energy theorem):

$$W=\mathrm{\Delta }K$$

---

Step 1: Expression for kinetic energy

$$K=\frac{1}{2}m{v}^2$$Given:$$v=a{x}^{3\mathrm{/}2}\Rightarrow v^2=a^2{x}^3$$

$$K=\frac{1}{2}m{a}^2{x}^3$$

---

Step 2: Initial and final kinetic energies

• At $x=0$:

$$K_i=\frac{1}{2}m{a}^2(0{)}^3=0$$

• At $x=2$:

$$K_f=\frac{1}{2}\times 0.5\times (5{)}^2\times (2{)}^3$$

$$K_f=\frac{1}{4}\times 25\times 8$$

$$K_f=50\text{ J}$$

Step 3: Work done

$$W=K_f-K_i=50-0$$

---

Question 5.21

The blades of a windmill sweep out a circle of area A.

(a) If the wind flows with velocity v perpendicular to the circle, what is the mass of air passing through it in time t?
(b) What is the kinetic energy of the air?
(c) Assume that the windmill converts 25% of the wind’s energy into electrical energy.
Given:

$$A=30{\text{ m}}^2,v=36{\text{ km h}}^{-1},\rho =1.2{\text{ kg m}}^{-3}$$

Find the electrical power produced.

---

Solution

(a) Mass of air passing in time $t$

In time $t$, air travels a distance $vt$.
Volume of air crossing the area:

$$V=Avt$$

Mass of air:

$$m=\rho V=\rho Avt$$

$$\boxed{{\displaystyle m=\rho Avt}}$$

---

(b) Kinetic energy of the air

$$K=\frac{1}{2}m{v}^2$$

Substitute $m=\rho Avt$:

$$K=\frac{1}{2}\rho Avt{v}^2$$

$$\boxed{{\displaystyle K=\frac{1}{2}\rho A{v}^{3}t}}$$

---

(c) Electrical power produced

First convert speed:

$$v=36{\text{ km h}}^{-1}=10{\text{ m s}}^{-1}$$

Power available in the wind

$$P_{\text{wind}}=\frac{K}{t}=\frac{1}{2}\rho A{v}^3$$

$$P_{\text{wind}}=\frac{1}{2}\times 1.2\times 30\times (10{)}^3$$

$$P_{\text{wind}}=0.6\times 30\times 1000=18000\text{ W}$$

Electrical power produced (25% efficiency)

$$P_{\text{electric}}=0.25\times 18000$$

$$\boxed{{\displaystyle P_{\text{electric}}=4500\text{ W}=4.5\text{ kW}}}$$

---

Question 5.22

A person trying to lose weight (dieter) lifts a 10 kg mass, 1000 times, to a height of 0.5 m each time. Assume that the potential energy lost each time she lowers the mass is dissipated.

(a) How much work does she do against the gravitational force?
(b) Fat supplies $3.8\times {10}^7$ J of energy, which is converted to mechanical energy with 20% efficiency. How much fat will the dieter use up?

---

Solution

Given

• Mass lifted, $m=10$

• Height each time, $h=0.5$

• Number of lifts, $n=1000$

• $g=10$

• Energy from fat = $3.8\times {10}^7$

• Efficiency, $\eta =20\mathrm{\%}=0.20$

---

(a) Work done against gravity

Work done in one lift:

$$W_1=mgh=10\times 10\times 0.5=50\text{ J}$$

Work done in 1000 lifts:

$$W=1000\times 50=5.0\times {10}^4\text{ J}$$

(The energy lost while lowering is dissipated, so it does not cancel this work.)

(b) Fat consumed

Only 20% of the energy from fat is converted into useful mechanical work.

So, energy obtained from fat:

$$E_{\text{fat}}=\frac{W}{\eta }=\frac{5.0\times {10}^4}{0.20}=2.5\times {10}^5\text{ J}$$

Mass of fat used:$$m_{\text{fat}}=\frac{E_{\text{fat}}}{3.8\times {10}^7}$$

$$m_{\text{fat}}=\frac{2.5\times {10}^5}{3.8\times {10}^7}\approx 6.6\times {10}^{-3}\text{ kg}$$

$$\boxed{{\displaystyle m_{\text{fat}}\approx 6.6\text{ g}}}$$

---

Question 5.23

A family uses 8 kW of power.

(a) Direct solar energy is incident on a horizontal surface at an average rate of
200 W m⁻². If 20% of this energy can be converted to useful electrical energy, how large an area is needed to supply 8 kW?

(b) Compare this area to that of the roof of a typical house.

---

Solution

(a) Area required

Solar power incident per unit area:

$$P_{\text{incident}}=200{\text{W m}}^{-2}$$

Useful electrical power obtained (20% efficiency):

$$P_{\text{useful}}=0.20\times 200=40{\text{W m}}^{-2}$$

Required power:

$$P=8\text{ kW}=8000\text{ W}$$

Area needed:

$$A=\frac{P}{P_{\text{useful}}}=\frac{8000}{40}=200{\text{m}}^2$$

$$\boxed{{\displaystyle A=200{\text{m}}^2}}$$

---

(b) Comparison with a typical house roof

The roof area of a typical house is about 100–150 m².

• Required area = 200 m²

• This is larger than the roof area of a typical house.

$$\boxed{{\displaystyle \text{Thus, the required area is comparable to,}}}$$

$$\boxed{{\displaystyle \text{but somewhat larger than, a typical house roof.}}}$$