Class 11th Physics Chapter-8 Solutions

Mechanical Properties of Solids

Question 8.1

A steel wire of length 4.7 m and cross-sectional area 3.0 × 10⁻⁵ m² stretches by the same amount as a copper wire of length 3.5 m and cross-sectional area 4.0 × 10⁻⁵ m² when both are subjected to the same load. Find the ratio of the Young’s modulus of steel to that of copper.

---

Solution

For a wire under tension, the extension is given by:

$$\mathrm{\Delta }L=\frac{FL}{AY}$$

Since both wires experience the same load and same extension,

$$\frac{F{L}_s}{A_s{Y}_s}=\frac{F{L}_c}{A_c{Y}_c}$$

Cancelling $F$ and rearranging,

$$\frac{Y_s}{Y_c}=\frac{L_s{A}_c}{L_c{A}_s}$$

Substituting values:

$$\frac{Y_s}{Y_c}=\frac{(4.7)(4.0\times {10}^{-5})}{(3.5)(3.0\times {10}^{-5})}$$

$$=\frac{18.8}{10.5}=1.79\approx 1.8$$

---

Question 8.2

Figure 8.9 shows the stress–strain curve for a given material.
Find:

1. Young’s modulus of the material, and

2. Approximate yield strength.

---

Understanding the Graph (Figure 8.9)

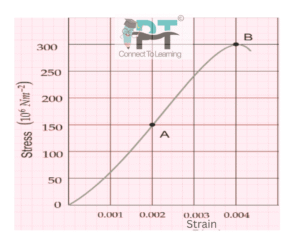
• X-axis: Strain (dimensionless)

• Y-axis: Stress (in MPa)

• The curve is linear initially and then bends after a point.

The linear portion obeys Hooke’s law and its slope gives Young’s modulus.
The point where the curve deviates from linearity gives the yield strength.

---

(a) Young’s Modulus

From the straight-line portion of the graph (approximate reading):

• Stress ≈ 150 MPa

• Corresponding strain ≈ 0.002

$$\text{Young’s modulus }(Y)=\frac{\text{Stress}}{\text{Strain}}$$
$$Y=\frac{150\text{ MPa}}{0.002}=\mathrm{75,000}\text{ MPa}=7.5\times {10}^{10}{\text{ N m}}^{-2}$$

Young’s Modulus

$$\boxed{{\displaystyle Y\approx 7.5\times {10}^{10}{\text{ N m}}^{-2}}}$$

---

(b) Approximate Yield Strength

• Yield point is where the curve starts deviating from linearity

• From the graph, this occurs at stress ≈ 250 MPa

Yield Strength

$$\boxed{{\displaystyle \text{Yield strength}\approx 250\text{ MPa}}}$$

---

Question 8.3

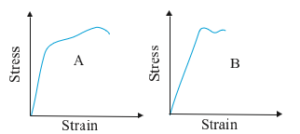
The stress–strain graphs for materials A and B are shown in Fig. 8.10.
The graphs are drawn to the same scale.

(a) Which of the materials has the greater Young’s modulus?
(b) Which of the two is the stronger material?

---

Solution

Key Concepts Used

1. Young’s Modulus (Y)

   • Equal to the slope of the linear (elastic) part of the stress–strain curve.

   • Steeper slope ⇒ larger Young’s modulus.

2. Strength of a Material

   • Determined by the maximum stress the material can withstand before breaking.

   • Higher maximum stress ⇒ stronger material.

---

(a) Greater Young’s Modulus

• From Fig. 8.10, material B has a steeper initial (linear) portion of the stress–strain curve than material A.

• Since:

  $$Y=\frac{\text{Stress}}{\text{Strain}}$$

  a steeper slope means larger Young’s modulus.

 Answer (a):

$$\boxed{{\displaystyle \text{Material B has the greater Young’s modulus}}}$$

(b) Stronger Material

• Strength depends on the maximum stress reached before fracture.

• From the graph, material A can withstand a higher stress before breaking than material B.

Answer (b):

$$\boxed{{\displaystyle \text{Material A is the stronger material}}}$$

---

Question 8.4

Read the following statements carefully and state, with reasons, whether they are true or false:

(a) The Young’s modulus of rubber is greater than that of steel.
(b) The stretching of a coil is determined by its shear modulus.

---

Solution

(a) The Young’s modulus of rubber is greater than that of steel.

❌ False

Reason:

• Young’s modulus is a measure of stiffness (resistance to deformation).

• Rubber stretches much more than steel for the same applied force.

• Hence, rubber has a much smaller Young’s modulus compared to steel.

Conclusion:
Steel is more elastic (stiffer) than rubber, even though rubber stretches more.

---

(b) The stretching of a coil is determined by its shear modulus.

✅ True

Reason:

• When a coil (spring) is stretched, the wire forming the coil undergoes shearing deformation, not longitudinal stretching.

• Therefore, the restoring force and extension of a coil depend on the shear modulus (modulus of rigidity) of the material.

---

Question 8.5

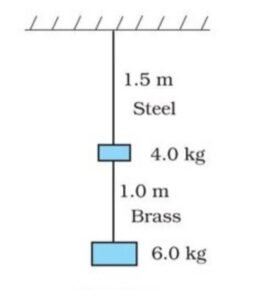
Two wires of equal diameter 0.25 cm, one made of steel and the other of brass, are loaded as shown in Fig. 8.11. The unloaded length of the steel wire is 1.5 m and that of the brass wire is 1.0 m.

Calculate the elongations of the steel wire and the brass wire.

(Young’s modulus: Steel = $2.0\times {10}^{11}{\text{N m}}^{-2}$,
Brass = $9.0\times {10}^{10}{\text{N m}}^{-2}$)

---

Solution

Given

Diameter of each wire:

$$d=0.25\text{ cm}=2.5\times {10}^{-3}\text{ m}$$

Radius:

$$r=1.25\times {10}^{-3}\text{ m}$$

Cross-sectional area:

$$A=\pi r^2=\pi (1.25\times {10}^{-3}{)}^2=4.9\times {10}^{-6}{\text{ m}}^2$$

Lengths:

• Steel wire: $L_s=1.5\text{ m}$

• Brass wire: $L_b=1.0\text{ m}$

Young’s modulus:

• Steel: $Y_s=2.0\times {10}^{11}{\text{ N m}}^{-2}$

• Brass: $Y_b=9.0\times {10}^{10}{\text{ N m}}^{-2}$

Load on each wire (from Fig. 8.11):

$$F=100\text{ N}$$

Formula Used

$$\mathrm{\Delta }L=\frac{FL}{AY}$$

(a) Elongation of Steel Wire

$$\mathrm{\Delta }{L}_s=\frac{(100)(1.5)}{(4.9\times {10}^{-6})(2.0\times {10}^{11})}$$

$$\mathrm{\Delta }{L}_s=1.53\times {10}^{-4}\text{ m}=0.153\text{ mm}$$

(b) Elongation of Brass Wire

$$\mathrm{\Delta }{L}_b=\frac{(100)(1.0)}{(4.9\times {10}^{-6})(9.0\times {10}^{10})}$$

$$\mathrm{\Delta }{L}_b=2.27\times {10}^{-4}\text{ m}=0.227\text{ mm}$$

---

Question 8.7

Four identical hollow cylindrical columns of mild steel support a big structure of mass 50,000 kg. The inner radius of each column is 30 cm and the outer radius is 60 cm. Assuming that the load is uniformly distributed, calculate the compressional strain of each column.

(Young’s modulus of mild steel = $2.0\times {10}^{11}{\text{N m}}^{-2}$;
take $g=9.8{\text{m s}}^{-2}$)

---

Solution

Step 1: Total load on the structure

$$W=mg=\mathrm{50,000}\times 9.8=4.9\times {10}^5\text{ N}$$

Since there are four identical columns, load on each column:

$$F=\frac{4.9\times {10}^5}{4}=1.225\times {10}^5\text{ N}$$

Step 2: Cross-sectional area of one hollow column

Outer radius:

$$R=60\text{ cm}=0.6\text{ m}$$

Inner radius:

$$r=30\text{ cm}=0.3\text{ m}$$

$$A=\pi (R^2-r^2)=\pi ({0.6}^2-{0.3}^2)$$

$$A=\pi (0.36-0.09)=\pi (0.27)=0.848{\text{ m}}^2$$

Step 3: Stress on each column

$$\text{Stress}=\frac{F}{A}=\frac{1.225\times {10}^5}{0.848}$$

$$\text{Stress}\approx 1.44\times {10}^5{\text{ N m}}^{-2}$$

Step 4: Compressional strain

$$\text{Strain}=\frac{\text{Stress}}{Y}$$

$$\text{Strain}=\frac{1.44\times {10}^5}{2.0\times {10}^{11}}$$

$$\text{Strain}=7.2\times {10}^{-7}$$

---

Question 8.8

A piece of copper having a rectangular cross-section of 15.2 mm × 19.1 mm is pulled in tension by a force of 44,500 N, producing only elastic deformation.
Calculate the resulting strain.

(Young’s modulus of copper = $1.1\times {10}^{11}{\text{N m}}^{-2}$)

---

Solution

Step 1: Given data

Force applied:

$$F=\mathrm{44,500}\text{ N}$$

Cross-sectional dimensions:

$$15.2\text{ mm}=15.2\times {10}^{-3}\text{ m}$$

$$19.1\text{ mm}=19.1\times {10}^{-3}\text{ m}$$

Cross-sectional area:

$$A=(15.2\times {10}^{-3})(19.1\times {10}^{-3})=2.9032\times {10}^{-4}{\text{ m}}^2$$

Young’s modulus of copper:

$$Y=1.1\times {10}^{11}{\text{ N m}}^{-2}$$

Step 2: Calculate stress

$$\text{Stress}=\frac{F}{A}=\frac{\mathrm{44,500}}{2.9032\times {10}^{-4}}$$

$$\text{Stress}\approx 1.53\times {10}^8{\text{ N m}}^{-2}$$

Step 3: Calculate strain

$$\text{Strain}=\frac{\text{Stress}}{Y}=\frac{1.53\times {10}^8}{1.1\times {10}^{11}}$$

$$\text{Strain}\approx 1.39\times {10}^{-3}$$

---

Question 8.9

A steel cable of radius 1.5 cm supports a chairlift at a ski area.
If the maximum stress in the cable is not to exceed

$$1.0\times {10}^8{\text{N m}}^{-2},$$

calculate the maximum load that the cable can support.

---

Solution

Step 1: Given data

Radius of cable:

$$r=1.5\text{ cm}=1.5\times {10}^{-2}\text{ m}$$

Maximum allowable stress:

$${\sigma }_{\max }=1.0\times {10}^8{\text{ N m}}^{-2}$$

Step 2: Cross-sectional area of the cable

$$A=\pi r^2=\pi (1.5\times {10}^{-2}{)}^2$$

$$A=\pi (2.25\times {10}^{-4})\approx 7.07\times {10}^{-4}{\text{ m}}^2$$

Step 3: Maximum load supported

Stress is given by:

$$\sigma =\frac{F}{A}$$

$$F_{\max }={\sigma }_{\max }\times A$$

$$F_{\max }=(1.0\times {10}^8)(7.07\times {10}^{-4})$$

$$F_{\max }\approx 7.07\times {10}^4\text{ N}$$

---

Question 8.10

A rigid bar of mass 15 kg is supported symmetrically by three vertical wires, each of length 2.0 m. The two end wires are of copper, while the middle wire is of iron. Determine the ratio of the diameters of the copper and iron wires if each wire is to have the same tension.

(Young’s modulus:
Copper $=1.1\times {10}^{11}{\text{N m}}^{-2}$,
Iron $=2.0\times {10}^{11}{\text{N m}}^{-2}$)

---

Solution

Key Physical Idea

• The bar is rigid and supported symmetrically, so for the bar to remain horizontal:

  • All three wires must undergo the same extension.

• The tension in each wire is the same (given condition).

---

Step 1: Use the extension formula

For a stretched wire:

$$\mathrm{\Delta }L=\frac{FL}{AY}$$

Here:

• $F$ = tension (same for all wires)

• $L$ = length (same for all wires)

• $A$ = cross-sectional area

• $Y$ = Young’s modulus

---

Step 2: Condition for equal extension

Since $\mathrm{\Delta }L$ is same for copper and iron wires:

$$\frac{FL}{A_c{Y}_c}=\frac{FL}{A_i{Y}_i}$$

Cancelling $F$ and $L$:

$$A_c{Y}_c=A_i{Y}_i$$

Step 3: Express area in terms of diameter

$$A=\frac{\pi d^2}{4}$$

So,$$d_c^2{Y}_c=d_i^2{Y}_i$$
$$\frac{d_c}{d_i}=\sqrt{\frac{Y_i}{Y_c}}$$

Step 4: Substitute values

$$\frac{d_c}{d_i}=\sqrt{\frac{2.0\times {10}^{11}}{1.1\times {10}^{11}}}=\sqrt{1.82}\approx 1.35$$

---

Question 8.11

A mass of 14.5 kg, fastened to the end of a steel wire of unstretched length 1.0 m, is whirled in a vertical circle. At the lowest point of the circle, the angular speed is 2 revolutions per second. The cross-sectional area of the wire is 0.065 cm².

Calculate the elongation of the wire when the mass is at the lowest point of its path.

(Young’s modulus of steel = $2.0\times {10}^{11}{\text{N m}}^{-2}$)

---

Solution

Step 1: Given data

Mass:

$$m=14.5\text{ kg}$$

Length of wire:$$L=1.0\text{ m}$$

Angular speed:

$$f=2\text{ rev/s}$$

$$\omega =2\pi f=4\pi \text{ rad/s}$$

Cross-sectional area:

$$A=0.065{\text{ cm}}^2=0.065\times {10}^{-4}{\text{ m}}^2=6.5\times {10}^{-6}{\text{ m}}^2$$

Young’s modulus of steel:

$$Y=2.0\times {10}^{11}{\text{ N m}}^{-2}$$

---

Step 2: Forces acting at the lowest point

At the lowest point, tension $T$ provides:

• Centripetal force

• Weight support

$$T-mg=m{\omega }^{2}r$$Here $r\approx L=1.0\text{ m}$

$$T=m{\omega }^{2}L+mg$$

Substitute values:

$$T=14.5\times (4\pi {)}^2\times 1.0+14.5\times 9.8$$

$$T=14.5\times 16{\pi }^2+142.1$$

$$T\approx 14.5\times 157.9+142.1$$

$$T\approx 2290+142$$

$$T\approx 2432\text{ N}$$

Step 3: Formula for elongation

$$\mathrm{\Delta }L=\frac{TL}{AY}$$

Step 4: Substitute values

$$\mathrm{\Delta }L=\frac{2432\times 1.0}{(6.5\times {10}^{-6})(2.0\times {10}^{11})}$$

$$\mathrm{\Delta }L=\frac{2432}{1.3\times {10}^6}$$

$$\mathrm{\Delta }L\approx 1.87\times {10}^{-3}\text{ m}$$

---

Question 8.12

Compute the bulk modulus of water from the following data:

• Initial volume of water = 100.0 litre

• Final volume of water = 100.5 litre

• Increase in pressure = 100.0 atm

  $$(1\text{ atm}=1.013\times {10}^5\text{ Pa})$$

Also, compare the bulk modulus of water with that of air (at constant temperature) and explain in simple terms why the ratio is so large.

---

Solution

Step 1: Convert given quantities into SI units

Initial volume:

$$V=100.0\text{ litre}=0.100{\text{ m}}^3$$

Final volume:

$$V_f=100.5\text{ litre}$$

Change in volume:

$$\mathrm{\Delta }V=100.5-100.0=0.5\text{ litre}=5.0\times {10}^{-4}{\text{ m}}^3$$

Increase in pressure:

$$\mathrm{\Delta }P=100.0\times 1.013\times {10}^5=1.013\times {10}^7\text{ Pa}$$

Step 2: Formula for bulk modulus

$$B=\frac{\mathrm{\Delta }P}{\mathrm{\Delta }V\mathrm{/}V}$$

Step 3: Substitute values

$$\frac{\mathrm{\Delta }V}{V}=\frac{5.0\times {10}^{-4}}{0.100}=5.0\times {10}^{-3}$$

$$B=\frac{1.013\times {10}^7}{5.0\times {10}^{-3}}$$

$$B\approx 2.03\times {10}^9\text{ Pa}$$

---

(a) Bulk Modulus of Water

$$\boxed{{\displaystyle B_{\text{water}}\approx 2.0\times {10}^9{\text{ N m}}^{-2}}}$$

(This agrees well with the standard value.)

---

(b) Comparison with Bulk Modulus of Air

• Bulk modulus of air (at constant temperature):

  $$B_{\text{air}}\approx 1.0\times {10}^5{\text{ N m}}^{-2}$$

Ratio

$$\frac{B_{\text{water}}}{B_{\text{air}}}=\frac{2.0\times {10}^9}{1.0\times {10}^5}=2.0\times {10}^4$$

$$\boxed{{\displaystyle B_{\text{water}}\approx \mathrm{20,000}\times B_{\text{air<span class="vlist" style="font-size: revert; font-family: var(--wp--preset--font-family--manrope); letter-spacing: -0.1px;"><span class="boxpad"><span class="msupsub"><span class="vlist-s"></span></span></span></span><span class="vlist-s" style="font-size: revert; font-family: var(--wp--preset--font-family--manrope); letter-spacing: -0.1px;"></span>}}}}$$

(c) Explanation (Why is the ratio so large?)

• In liquids (water), molecules are closely packed with very little empty space.

• Hence, liquids are very difficult to compress, giving a very large bulk modulus.

• In gases (air), molecules are far apart, so gases compress easily.

• Therefore, air has a very small bulk modulus compared to water.

---

Question 8.13

What is the density of water at a depth where the pressure is 80.0 atm, given that the density of water at the surface is

$$1.03\times {10}^3{\text{kg m}}^{-3}?$$

(Bulk modulus of water $=2.2\times {10}^9{\text{N m}}^{-2}$;
$1\text{ atm}=1.013\times {10}^5\text{ Pa}$)

---

Solution

Step 1: Given data

Density at surface:

$${\rho }_0=1.03\times {10}^3{\text{kg m}}^{-3}$$Pressure at depth:

$$\mathrm{\Delta }P=80.0\text{ atm}=80\times 1.013\times {10}^5=8.10\times {10}^6\text{ Pa}$$

Bulk modulus of water:

$$B=2.2\times {10}^9{\text{N m}}^{-2}$$

Step 2: Relation between density and bulk modulus

$$B=\frac{\mathrm{\Delta }P}{\mathrm{\Delta }\rho \mathrm{/}\rho }$$

$$\Rightarrow \frac{\mathrm{\Delta }\rho }{\rho }=\frac{\mathrm{\Delta }P}{B}$$

Step 3: Calculate fractional change in density

$$\frac{\mathrm{\Delta }\rho }{\rho }=\frac{8.10\times {10}^6}{2.2\times {10}^9}\approx 3.68\times {10}^{-3}$$

Step 4: Calculate change in density

$$\mathrm{\Delta }\rho ={\rho }_0\times \frac{\mathrm{\Delta }\rho }{\rho }$$

$$\mathrm{\Delta }\rho =(1.03\times {10}^3)\times (3.68\times {10}^{-3})\approx 3.8{\text{kg m}}^{-3}$$

Step 5: Density at depth

$$\rho ={\rho }_0+\mathrm{\Delta }\rho =1030+3.8$$

$$\rho \approx 1.034\times {10}^3{\text{kg m}}^{-3}$$

---

Question 8.14

Compute the fractional change in volume of a glass slab when it is subjected to a hydraulic pressure of 10 atm.

(Bulk modulus of glass $=3.7\times {10}^{10}{\text{N m}}^{-2}$;
$1\text{ atm}=1.013\times {10}^5\text{ Pa}$)

---

Solution

Step 1: Given data

Pressure applied:

$$\mathrm{\Delta }P=10\text{ atm}=10\times 1.013\times {10}^5=1.013\times {10}^6\text{ Pa}$$

Bulk modulus of glass:

$$B=3.7\times {10}^{10}{\text{N m}}^{-2}$$

Step 2: Formula for bulk modulus

$$B=\frac{\mathrm{\Delta }P}{\mathrm{\Delta }V\mathrm{/}V}$$

$$\Rightarrow \frac{\mathrm{\Delta }V}{V}=\frac{\mathrm{\Delta }P}{B}$$

Step 3: Substitute values

$$\frac{\mathrm{\Delta }V}{V}=\frac{1.013\times {10}^6}{3.7\times {10}^{10}}$$

$$\frac{{\mathrm{<span\; style="font-size:\; revert;\; font-family:\; var(--wp--preset--font-family--manrope);\; letter-spacing:\; -0.1px;"></span>}}^{}}{}$$$$\frac{\mathrm{\Delta }V}{V}\approx 2.74\times {10}^{-5}$$

---

Question 8.15

Determine the volume contraction of a solid copper cube, each edge of which is 10 cm, when it is subjected to a hydraulic pressure of $7.0\times {10}^6\text{Pa}$.

(Bulk modulus of copper $=1.4\times {10}^{11}{\text{N m}}^{-2}$)

---

Solution

Step 1: Given data

Edge of the cube:

$$a=10\text{ cm}=0.10\text{ m}$$Initial volume:

$$V=a^3=(0.10{)}^3=1.0\times {10}^{-3}{\text{m}}^3$$

Applied pressure:

$$\mathrm{\Delta }P=7.0\times {10}^6\text{ Pa}$$

Bulk modulus of copper:

$$B=1.4\times {10}^{11}{\text{N m}}^{-2}$$

Step 2: Formula used

Bulk modulus is given by:

$$B=\frac{\mathrm{\Delta }P}{\mathrm{\Delta }V\mathrm{/}V}$$Rearranging,

$$\mathrm{\Delta }V=\frac{\mathrm{\Delta }P}{B}\times V$$

Step 3: Substitute values

$$\mathrm{\Delta }V=\frac{7.0\times {10}^6}{1.4\times {10}^{11}}\times 1.0\times {10}^{-3}$$

$$\mathrm{\Delta }V=5.0\times {10}^{-8}{\text{m}}^3$$

---

Question 8.16

How much should the pressure on one litre of water be changed so as to compress it by 0.10%?

(Bulk modulus of water $=2.2\times {10}^9{\text{N m}}^{-2}$)

---

Solution

Step 1: Given data

Volume of water:

$$V=1\text{ litre}$$

(Note: actual volume value is not required because we are given fractional change.)

Fractional change in volume:

$$\frac{\mathrm{\Delta }V}{V}=0.10\mathrm{\%}=\frac{0.10}{100}=1.0\times {10}^{-3}$$

Bulk modulus of water:

$$B=2.2\times {10}^9{\text{N m}}^{-2}$$

Step 2: Formula for bulk modulus

$$B=\frac{\mathrm{\Delta }P}{\mathrm{\Delta }V\mathrm{/}V}$$

Rearranging,

$$\mathrm{\Delta }P=B\times \frac{\mathrm{\Delta }V}{V}$$

Step 3: Substitute values

$$\mathrm{\Delta }P=(2.2\times {10}^9)\times (1.0\times {10}^{-3})$$

$$\mathrm{\Delta }P=2.2\times {10}^6\text{ Pa}$$