Go Back to Class 12th Physics
Question 1.1
What is the force between two small charged spheres having charges and placed 30 cm apart in air?
Solution
Given:
Distance,
-
Medium: air (same as vacuum)
Formula (Coulomb’s Law):
where
Calculation:
Question 1.2
The electrostatic force on a small sphere of charge
due to another small sphere of charge in air is
.(a) What is the distance between the two spheres?
(b) What is the force on the second sphere due to the first?
Solution
Given:
Force,
Medium: air (same as vacuum)
(a) Distance between the two spheres
Formula (Coulomb’s Law):
Substitution:
Question 1.3
Check that the ratio
is dimensionless. Look up a table of physical constants and determine the value of this ratio. What does the ratio signify?
Solution
(a) Checking whether the ratio is dimensionless
Write the units of each quantity:
; Units:
(electronic charge) Units: C
(gravitational constant) Units:
(masses of electron and proton) – Units: kg
Now, units of the numerator:
Units of the denominator:
So, the ratio is:
Hence, the ratio is dimensionless.
(b) Numerical value of the ratio
Using standard physical constants:
Substitute:
(c) Physical significance of the ratio
-
This ratio represents the ratio of electrostatic force to gravitational force between an electron and a proton.
The value is extremely large (), which shows that:
-
Gravity is negligible at the atomic and subatomic scale compared to electric forces.
Question 1.4
(a) Explain the meaning of the statement “electric charge of a body is quantised”.
(b) Why can one ignore quantisation of electric charge when dealing with macroscopic (large-scale) charges?
Answer
(a) Meaning of quantisation of electric charge
The statement “electric charge is quantised” means that:
-
Electric charge exists in discrete packets, not in a continuous manner.
- The charge
on any body is always an integral multiple of a fundamental unit of charge .
Mathematically,
where:
(magnitude of charge on an electron or proton)
✔ Hence, electric charge is quantised.
(b) Why quantisation of charge can be ignored for macroscopic charges
In macroscopic (large-scale) situations:
-
The amount of charge involved is usually of the order of microcoulombs (μC) or coulombs (C).
-
Such charges contain a very large number of electrons.
For example:
Compared to this huge number:
-
The elementary charge
is extremely small.
-
Any change in charge by one electron is negligible.
✔ Hence, quantisation of electric charge can be ignored for large-scale charges.
Question 1.5
When a glass rod is rubbed with a silk cloth, charges appear on both.
A similar phenomenon is observed with many other pairs of bodies.
Explain how this observation is consistent with the law of conservation of charge.
Answer
The law of conservation of charge states that:
Electric charge can neither be created nor destroyed; it can only be transferred from one body to another.
When a glass rod is rubbed with a silk cloth, electrons are transferred from the glass rod to the silk cloth. As a result, the glass rod becomes positively charged and the silk cloth becomes negatively charged. No new charge is created; the charge lost by the glass rod is equal to the charge gained by the silk cloth.
Thus, the total charge of the system remains conserved, which is consistent with the law of conservation of charge.
Question 1.6
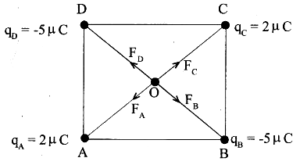
Four point charges
are located at the corners of a square ABCD of side 10 cm.
What is the force on a charge of
placed at the centre of the square?
Solution
Using symmetry:
- The distance from the centre to each corner of the square is the same.
- The charges at opposite corners are equal:
Forces due to opposite corners:
Force on the central charge due to
is equal in magnitude and opposite in direction to that due to
⇒ they cancel.
Force due to is equal in magnitude and opposite in direction to that due to
⇒ they cancel.
Since each pair of opposite forces cancels, the vector sum of all forces is zero.
Question 1.7
(a) An electrostatic field line is a continuous curve. That is, a field line cannot have sudden breaks. Why not?
(b) Explain why two field lines never cross each other at any point.
Answer
(a) Why an electrostatic field line cannot have sudden breaks
An electrostatic field line represents the direction of the electric field at every point in space.
The electric field exists continuously in space (except at the location of charges).
-
If a field line had a sudden break, it would imply that the electric field suddenly disappears at that point.
-
This is not possible because an electric field cannot start or stop abruptly in free space.
✔ Therefore, electrostatic field lines must be continuous curves, starting from positive charges and ending on negative charges (or at infinity).
(b) Why two field lines never cross each other
-
The direction of the electric field at a point is unique.
-
A field line at any point gives the direction of the electric field at that point.
If two field lines crossed:
-
There would be two different tangents at the point of intersection.
-
This would mean two different directions of the electric field at the same point, which is impossible.
✔ Hence, two electric field lines can never cross each other.
Question 1.8
Two point charges
and are located 20 cm apart in vacuum.
(a) What is the electric field at the midpoint of the line AB joining the two charges?
(b) If a negative test charge of magnitude is placed at this point, what is the force experienced by the test charge?
Solution
Given:
Distance AB = 20 cm ⇒ distance of each charge from midpoint
(a) Electric field at midpoint
Electric field due to a point charge:
Field due to at :
Field due to at :
Direction:
- Field due to is away from A (towards B) +
Thus, both fields are in the same direction (from A to B).
Answer (a):
(b) Force on the test charge
Given test charge:
Force on a charge in an electric field:
The negative sign indicates that the force is opposite to the direction of the electric field.
Answer (b):
Question 1.9
A system has two charges
(a) Total charge of the system
(b) Electric dipole moment of the system
Solution
(a) Total charge of the system
✔ The system is electrically neutral.
(b) Electric dipole moment
Electric dipole moment:
where
q = 2.5 × 10 − 7 C d ⃗
Distance between charges:
So,
Direction:
From negative charge at
Question 1.10
An electric dipole with dipole moment
Solution
Formula (Torque on an electric dipole):
Substitution:
Question 1.11
A polythene piece rubbed with wool is found to have a negative charge of
(a) Estimate the number of electrons transferred (from which to which?).
(b) Is there a transfer of mass from wool to polythene?
Solution
(a) Number of electrons transferred
Given:
- Charge on polythene,
q = − 3 × 10 − 7 C - Charge of one electron,
e = 1.6 × 10 − 19 C
Number of electrons transferred:
Direction of transfer:
Since the polythene becomes negatively charged, electrons are transferred from wool to polythene.
(b) Is there a transfer of mass?
Yes.
Electrons have mass (
However, this mass is extremely small and negligible in practice.
Question 1.12
(a) Two insulated charged copper spheres A and B have their centres 50 cm apart. Charge on each sphere
(b) What is the force of repulsion if each charge is doubled and the distance is halved?
Solution
Given (a):
q 1 = q 2 = 6.5 × 10 − 7 C r = 50 cm = 0.50 m k = 1 4 π ε 0 = 9 × 10 9 N m 2 C − 2
Formula (Coulomb’s law):
Calculation (a):F = 9 × 10 9 × ( 6.5 × 10 − 7 ) 2 ( 0.50 ) 2
Answer (a):
(b) Effect of doubling charges and halving distance
New charges:
New distance:
Using proportionality:
Answer (b):
Question 1.13
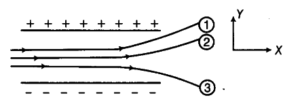
Figure 1.30 shows tracks of three charged particles in a uniform electrostatic field. Give the signs of the three charges. Which particle has the highest charge to mass ratio?
Understanding the situation
-
In a uniform electrostatic field,
-
Positive charges bend in the direction of the electric field
-
Negative charges bend opposite to the direction of the electric field
-
-
A neutral particle would move straight (no bending).
-
The amount of bending (curvature) depends on the charge to mass ratio (q/m):
-
Greater curvature → larger q/m
-
Smaller curvature → smaller q/m
-
Signs of the charges
From Figure 1.30 :
-
Particle 1 bends upward (along the electric field)
→ Positively charged -
Particle 2 bends downward (opposite to the field)
→ Negatively charged -
Particle 3 bends upward (same direction as Particle 1)
→ Positively charged
Signs of charges
-
Particle 1: Positive
-
Particle 2: Negative
-
Particle 3: Positive
Highest charge to mass ratio (q/m)
-
The particle whose path shows the maximum curvature has the highest q/m ratio.
-
From the figure, Particle 2 bends the most.
Question 1.14
Consider a uniform electric field
(a) What is the flux of this field through a square of side 10 cm whose plane is parallel to the yz-plane?
(b) What is the flux through the same square if the normal to its plane makes a 60° angle with the x-axis?
Given
-
Electric field:
E = 3 × 10 3 N/C (along +x direction) -
Side of square:
a = 10 cm = 0.10 m -
Area of square:
A = a 2 = ( 0.10 ) 2 = 0.01 m 2 -
Formula for electric flux:
Φ = E ⃗ ⋅ A ⃗ = E A cos θ where
θ
(a) Plane parallel to the yz-plane
-
Normal to the yz-plane is along the x-axis.
-
Electric field is also along the x-axis.
-
Therefore,
θ = 0 ∘ , cos 0 ∘ = 1
Calculation
(b) Normal makes 60° with the x-axis
-
Angle between
E ⃗ θ = 60 ∘ , cos 60 ∘ = 1 2
Calculation
Question 1.15
What is the net flux of the uniform electric field of Exercise 1.14 through a cube of side 20 cm oriented so that its faces are parallel to the coordinate planes?
Given
-
Uniform electric field (from Exercise 1.14):
E ⃗ = 3 × 10 3 i ^ N/C -
Side of cube:
a = 20 cm = 0.20 m -
Cube faces are parallel to coordinate planes.
-
The cube is a closed surface.
Concept Used
According to Gauss’s law,
-
A uniform electric field does not enclose any charge inside the cube.
-
Hence,
q enclosed = 0
Reasoning (Important for exams)
-
Electric flux entering the cube through one face is equal to the flux leaving through the opposite face.
-
Flux through the remaining four faces is zero because the electric field is parallel to those faces.
-
Therefore, all fluxes cancel out.
Question 1.16
Careful measurement of the electric field at the surface of a black box indicates that the net outward flux through the surface of the box is
(a) What is the net charge inside the box?
(b) If the net outward flux through the surface of the box were zero, could you conclude that there were no charges inside the box? Why or why not?
Concept Used: Gauss’s Law
(a) Net charge inside the box
Given
Using Gauss’s law:
(b) If the net outward flux were zero
Can we conclude that there are no charges inside the box?
Answer: No
Reason
-
Zero net flux means:
q enclosed = 0 -
This only tells us that the algebraic sum of charges inside is zero.
-
There may still be charges present, such as:
-
Equal positive and negative charges inside the box.
-
-
Their effects cancel, giving zero net flux.
Question 1.17
A point charge
Understanding the idea (key hint explained)
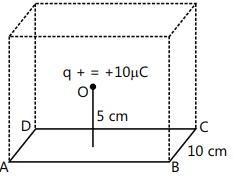
-
The square has side 10 cm.
-
The charge is 5 cm above the centre of the square.
-
If we imagine a cube of edge 10 cm, this square can be taken as one face of the cube.
-
Then the charge lies exactly at the centre of the cube.
This allows us to use Gauss’s law and symmetry.
Step 1: Total flux through the cube
By Gauss’s law,
Step 2: Flux through one face of the cube
-
A cube has 6 identical faces.
-
The charge is at the centre, so flux is equally distributed.
Question 1.18
A point charge of
Concept Used: Gauss’s Law
Given
-
Charge at centre:
q = 2.0 μ C = 2.0 × 10 − 6 C -
Permittivity of free space:
ε 0 = 8.85 × 10 − 12 C 2 / ( N m 2 )
(Note: The size of the cube is irrelevant for net flux.)
Calculation
Question 1.20
A conducting sphere of radius 10 cm has an unknown charge. If the electric field 20 cm from the centre of the sphere is
Given
-
Radius of sphere = 10 cm (not directly needed)
-
Distance from centre:
r = 20 cm = 0.20 m -
Electric field:
E = 1.5 × 10 3 N/C -
Direction of field: radially inward
Concept Used
Outside a conducting sphere, the electric field is the same as that due to a point charge at the centre.
Calculation
Sign of the charge
-
Electric field points radially inward
-
Therefore, the charge on the sphere must be negative
Question 1.21
A uniformly charged conducting sphere of diameter 2.4 m has a surface charge density of
(a) Find the charge on the sphere.
(b) What is the total electric flux leaving the surface of the sphere?
Given
-
Diameter of sphere = 2.4 m
⇒ r = 1.2 m -
Surface charge density:
σ = 80.0 μ C/m 2 = 80 × 10 − 6 C/m 2 -
Permittivity of free space:
ε 0 = 8.85 × 10 − 12 C 2 / ( N m 2 )
(a) Charge on the sphere
Surface area of a sphere:
Question 1.22
An infinite line charge produces an electric field of
Given
-
Electric field:
E = 9 × 10 4 N/C -
Distance from line charge:
r = 2 cm = 0.02 m -
Permittivity of free space:
ε 0 = 8.85 × 10 − 12 C 2 / ( N m 2 )
Concept Used: Gauss’s Law for an Infinite Line Charge
For an infinitely long straight charged wire,
where
Question 1.23
Two large, thin metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and of magnitude
Find the electric field
(a) in the outer region of the first plate,
(b) in the outer region of the second plate, and
(c) between the plates.
Concept Used
-
Electric field due to a single infinite sheet of charge:
-
For two parallel plates with equal and opposite surface charge densities:
-
Outside the plates → fields cancel
-
Between the plates → fields add
-
Given
(a) Electric field outside the first plate
-
Field due to the positively charged plate is canceled by the field due to the negatively charged plate.
(b) Electric field outside the second plate
-
Same reasoning as part (a).
(c) Electric field between the plates
-
Fields due to both plates are in the same direction and hence add.
CalculationE = 17.0 × 10 − 22 8.85 × 10 − 12