Class 12th Class 12th Maths
Question 15.
Show that height of the cylinder of greatest volume which can be inscribed in a right circular cone of height and semi-vertical angle is one-third that of the cone, and the greatest volume is .
Solution
Step 1: Geometry of the cone and the inscribed cylinder
Let a cylinder of
-
height =
-
radius =
be inscribed in a right circular cone of
-
height =
-
semi-vertical angle =
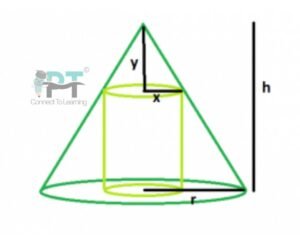
From the diagram:
The radius at height from the vertex is proportional to height:
Thus,
Step 2: Volume of the cylinder
Substitute (1):
Let:
Then,
Step 3: Differentiate to find maximum
Set :
Solve quadratic:
Possible values:
The cylinder cannot have height = (radius would be 0).
Hence the valid maximum is:
Thus the height of the cylinder of greatest volume is one-third that of the cone.
Step 4: Maximum radius
Use (1):
Step 5: Maximum Volume
Answers:-
Height of cylinder of greatest volume:
Greatest possible volume:
