Class 11th Physics Chapter-3 Solutions

Question 3.1 

State, for each of the following physical quantities, whether it is a scalar or a vector:

volume, mass, speed, acceleration, density, number of moles, velocity, angular frequency, displacement, angular velocity.

Answer

Exam-tip (1 line logic)

• Scalar → has magnitude only

• Vector → has magnitude + direction

• Triangle Law can be applied

---

Question 3.2 

Pick out the two scalar quantities in the following list :

force, angular momentum, work, current, linear momentum, electric field, average velocity, magnetic moment, relative velocity.

---

Answer

The two scalar quantities are:

$$\boxed{{\displaystyle \text{Work, }\text{ Current}}}$$

---

Question 3.3 

Pick out the only vector quantity in the following list :

Temperature, pressure, impulse, time, power, total path length, energy, gravitational potential, coefficient of friction, charge.

Answer

$$\boxed{{\displaystyle \text{Impulse}}}$$

Impulse = change in momentum, and momentum is a vector, hence impulse is a vector.

---

Question 3.4 

State with reasons whether the following algebraic operations with scalar and vector physical quantities are meaningful:

---

(a) Adding any two scalars

✅ Meaningful
Reason: Scalars have magnitude only and obey the rules of ordinary algebra (provided they have the same dimensions).
Example: 5 kg + 3 kg = 8 kg

---

(b) Adding a scalar to a vector of the same dimensions

❌ Not meaningful
Reason: Scalars and vectors are different types of physical quantities; a scalar has no direction while a vector has both magnitude and direction. They cannot be added.
Example: Mass (scalar) + displacement (vector) ❌

---

(c) Multiplying any vector by any scalar

✅ Meaningful
Reason: Multiplying a vector by a scalar changes its magnitude (and possibly its direction if the scalar is negative).
Example: 2 v, −3 F

---

(d) Multiplying any two scalars

✅ Meaningful
Reason: Scalars follow ordinary multiplication rules.
Example: Pressure × volume, mass × acceleration magnitude

---

(e) Adding any two vectors

❌ Not always meaningful
Reason: Two vectors can be added only if they represent the same physical quantity.
Example: Velocity + velocity ✔️, but velocity + force ❌

---

(f) Adding a component of a vector to the same vector

❌ Not meaningful
Reason: A component (e.g., $A_x$) is a scalar, while the vector $\vec{A}$ is a vector; scalar and vector cannot be added.
Example: $\vec{A}+A_x$ ❌

---

---

Question 3.5 

Read each statement below carefully and state with reasons whether it is true or false :

---

(a) The magnitude of a vector is always a scalar

✅ True
Reason: The magnitude gives only the size of the vector and has no direction, hence it is a scalar.
Example: Speed is the magnitude of velocity and is scalar.

---

(b) Each component of a vector is always a scalar

❌ False
Reason: The numerical component (like $A_x$) is a scalar, but the component vector (like $A_x\widehat{i}$) is a vector. Hence the statement is not always true.

---

(c) The total path length is always equal to the magnitude of the displacement vector of a particle

❌ False
Reason: Total path length depends on the actual path taken, whereas displacement depends only on initial and final positions.
Equality occurs only for straight-line motion without change in direction.

---

(d) The average speed of a particle is either greater than or equal to the magnitude of average velocity of the particle over the same time interval

✅ True
Reason:

$$\text{Average speed}=\frac{\text{total path length}}{t},\mathrm{\mid }\text{average velocity}\mathrm{\mid }=\frac{\mathrm{\mid }\text{displacement}\mathrm{\mid }}{t}$$

Since total path length ≥ displacement, average speed ≥ magnitude of average velocity.

---

(e) Three vectors not lying in a plane can never add up to give a null vector

✅ True
Reason: For vectors to add up to zero, they must form a closed polygon, which is possible only if they are coplanar.

---

Question 3.6 

Establish the following vector inequalities geometrically or otherwise :

$$\begin{array}{rl}{\displaystyle (a)}& {\displaystyle \mathrm{\mid }\mathbf{a}+\mathbf{b}\mathrm{\mid }<\mathrm{\mid }\mathbf{a}\mathrm{\mid }+\mathrm{\mid }\mathbf{b}\mathrm{\mid }}\\ {\displaystyle (b)}& {\displaystyle \mathrm{\mid }\mathbf{a}+\mathbf{b}\mathrm{\mid }>\mid \mathrm{\mid }\mathbf{a}\mathrm{\mid }-\mathrm{\mid }\mathbf{b}\mathrm{\mid }\mid }\\ {\displaystyle (c)}& {\displaystyle \mathrm{\mid }\mathbf{a}-\mathbf{b}\mathrm{\mid }<\mathrm{\mid }\mathbf{a}\mathrm{\mid }+\mathrm{\mid }\mathbf{b}\mathrm{\mid }}\\ {\displaystyle (d)}& {\displaystyle \mathrm{\mid }\mathbf{a}-\mathbf{b}\mathrm{\mid }>\mid \mathrm{\mid }\mathbf{a}\mathrm{\mid }-\mathrm{\mid }\mathbf{b}\mathrm{\mid }\mid }\end{array}$$

When does the equality sign above apply?

---

Answer:

Geometrical idea (triangle law)

If two vectors a and b are placed head-to-tail, they form two sides of a triangle; the resultant (a+b) is the third side. For any triangle:

• the length of one side is less than the sum of the other two,

• and greater than the difference of the other two.

---

(a) $\mathrm{\mid }\mathbf{a}+\mathbf{b}\mathrm{\mid }<\mathrm{\mid }\mathbf{a}\mathrm{\mid }+\mathrm{\mid }\mathbf{b}\mathrm{\mid }$

Reason: By the triangle law, the magnitude of the resultant side of a triangle is less than the sum of the magnitudes of the other two sides.
Equality holds only when a and b are in the same direction.

---

(b) $\mathrm{\mid }\mathbf{a}+\mathbf{b}\mathrm{\mid }>\mid \mathrm{\mid }\mathbf{a}\mathrm{\mid }-\mathrm{\mid }\mathbf{b}\mathrm{\mid }\mid$

Reason: In any triangle, one side is greater than the difference of the other two sides.
Equality holds when a and b are in opposite directions.

---

(c) $\mathrm{\mid }\mathbf{a}-\mathbf{b}\mathrm{\mid }<\mathrm{\mid }\mathbf{a}\mathrm{\mid }+\mathrm{\mid }\mathbf{b}\mathrm{\mid }$

Note that $\mathbf{a}-\mathbf{b}=\mathbf{a}+(-\mathbf{b})$

Reason: Applying result (a) to vectors a and −b, whose magnitude is $\mathrm{\mid }\mathbf{b}\mathrm{\mid }$:

$$\mathrm{\mid }\mathbf{a}-\mathbf{b}\mathrm{\mid }=\mathrm{\mid }\mathbf{a}+(-\mathbf{b})\mathrm{\mid }<\mathrm{\mid }\mathbf{a}\mathrm{\mid }+\mathrm{\mid }\mathbf{b}\mathrm{\mid }\mathrm{.}$$

---

(d) $\mathrm{\mid }\mathbf{a}-\mathbf{b}\mathrm{\mid }>\mid \mathrm{\mid }\mathbf{a}\mathrm{\mid }-\mathrm{\mid }\mathbf{b}\mathrm{\mid }\mid$

Reason: Applying result (b) to vectors a and −b:

$$\mathrm{\mid }\mathbf{a}-\mathbf{b}\mathrm{\mid }=\mathrm{\mid }\mathbf{a}+(-\mathbf{b})\mathrm{\mid }>\mid \mathrm{\mid }\mathbf{a}\mathrm{\mid }-\mathrm{\mid }\mathbf{b}\mathrm{\mid }\mid$$

Equality holds when the vectors are collinear (parallel), either in the same or opposite direction as required.

---

Question 3.7

Given

$$\mathbf{a}+\mathbf{b}+\mathbf{c}+\mathbf{d}=0$$

Which of the following statements are correct?

---

(a) $\mathbf{a},\mathbf{b},\mathbf{c},\mathbf{d}$ must each be a null vector

❌ False
Reason: Non-zero vectors can add up to zero if they form a closed polygon (e.g., a quadrilateral). Each vector need not be zero individually.

---

(b) The magnitude of $(\mathbf{a}+\mathbf{c})$ equals the magnitude of $(\mathbf{b}+\mathbf{d})$

✅ True
Reason: From the given condition,

$$\mathbf{a}+\mathbf{c}=-(\mathbf{b}+\mathbf{d})$$

Vectors equal in magnitude and opposite in direction have the same magnitude.

---

(c) The magnitude of $\mathbf{a}$ can never be greater than the sum of the magnitudes of $\mathbf{b},\mathbf{c},\mathbf{d}$

✅ True
Reason: From

$$\mathbf{a}=-(\mathbf{b}+\mathbf{c}+\mathbf{d})$$

Taking magnitudes and using the triangle inequality,

$$\mathrm{\mid }\mathbf{a}\mathrm{\mid }\le \mathrm{\mid }\mathbf{b}\mathrm{\mid }+\mathrm{\mid }\mathbf{c}\mathrm{\mid }+\mathrm{\mid }\mathbf{d}\mathrm{\mid }$$

---

(d) $\mathbf{b}+\mathbf{c}$ must lie in the plane of $\mathbf{a}$ and $\mathbf{d}$ if $\mathbf{a}$ and $\mathbf{d}$ are not collinear, and in the line of $\mathbf{a}$and $\mathbf{d}$ if they are collinear

✅ True
Reason: From

$$\mathbf{b}+\mathbf{c}=-(\mathbf{a}+\mathbf{d})$$

The vector $\mathbf{a}+\mathbf{d}$ lies:

• in the plane of a and d if they are not collinear,

• along the same line if they are collinear.

Hence $\mathbf{b}+\mathbf{c}$ must lie in the same plane or line respectively.

---

---

Question 3.8 

Three girls skating on a circular ice ground of radius 200 m start from a point P on the edge of the ground and reach a point Q diametrically opposite to P following different paths as shown in Fig. 3.19. What is the magnitude of the displacement vector for each? For which girl is this equal to the actual length of path skated?

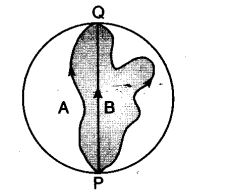
Answer

Magnitude of displacement

Displacement depends only on initial and final positions, not on the path taken.

• Points P and Q are diametrically opposite points on a circle of radius

  $$R=200\text{ m}$$

• Distance PQ = diameter of the circle

  $$PQ=2R=2\times 200=\boxed{{\displaystyle 400\text{ m}}}$$

✅ Magnitude of displacement for each girl = 400 m

---

Path length vs displacement

• Girl skating along the diameter (straight line PQ):

  • Actual path length = 400 m

  • Displacement = 400 m
    ✅ Path length equals displacement

• Girls skating along curved paths (arc or other curved routes):

  • Actual path length greater than 400 m

  • Displacement = 400 m
    ❌ Path length ≠ displacement

---

Question 3.9 

A cyclist starts from the centre O of a circular park of radius 1 km, reaches the edge P of the park, then cycles along the circumference, and returns to the centre along QO as shown in Fig. 3.20. If the round trip takes 10 min, find:

(a) net displacement
(b) average velocity
(c) average speed

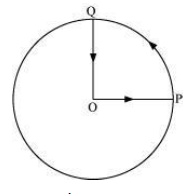
Given

• Radius of circular park, $R=1\text{km}$

• Total time, $t=10\text{min}={\displaystyle \frac{1}{6}}\text{h}$

---

(a) Net displacement

• Initial position = O (centre)

• Final position = O (centre)

$$\text{Net displacement}=0$$

---

(b) Average velocity

$$\text{Average velocity}=\frac{\text{Net displacement}}{\text{Total time}}$$

Since net displacement = 0,

$$\text{Average velocity}=0$$

---

(c) Average speed

First calculate the total distance travelled:

1. O to P (radius) = $1\text{km}$

2. Along circumference from P to Q = semicircle

   $$=\frac{1}{2}(2\pi R)=\pi R=\pi \times 1=\pi \text{km}$$

3. Q to O (radius) = $1\text{km}$

Total distance:

$$\text{Distance}=1+\pi +1=(2+\pi )\text{ km}$$

Average speed:

$$\text{Average speed}=\frac{2+\pi }{1\mathrm{/}6}=6(2+\pi )$$

$$\boxed{{\displaystyle \text{Average speed}=6(2+\pi ){\text{km h}}^{-1}\approx 30.8{\text{km h}}^{-1}}}$$

---

Question 3.10 

On an open ground, a motorist follows a track that turns to his left by an angle of ${60}^{\circ }$ after every 500 m. Starting from a given turn, specify the displacement of the motorist at the third, sixth and eighth turn. Compare the magnitude of the displacement with the total path length covered by the motorist in each case.

---

Understanding the motion

• Each straight segment = 500 m

• Turn after every segment = ${60}^{\circ }$ to the left

• This motion traces the sides of a regular hexagon (since exterior angle = ${60}^{\circ }$).

Let side length $s=500\text{m}$.

---

(i) Displacement at the 3rd turn

• After 3 sides of a regular hexagon, the motorist reaches the vertex opposite to the starting point.

• Displacement = distance between opposite vertices of a hexagon

$$=2s=2\times 500=\boxed{{\displaystyle 1000\text{ m}}}$$Path length covered:

$$3\times 500=\boxed{{\displaystyle 1500\text{ m}}}$$Comparison:

$$\text{Displacement (1000 m)}<\text{Path length (1500 m)}$$

---

(ii) Displacement at the 6th turn

• After 6 sides, the motorist completes one full hexagon and returns to the starting point.

$$\boxed{{\displaystyle \text{Displacement}=0}}$$Path length covered:

$$6\times 500=\boxed{{\displaystyle 3000\text{ m}}}$$Comparison:

$$\text{Displacement}=0\ll \text{Path length}$$

---

(iii) Displacement at the 8th turn

• 8 turns = 6 turns + 2 more turns

• Equivalent to displacement after 2 sides of the hexagon.

• Two vectors of magnitude $s$ at an angle of ${60}^{\circ }$.

Using vector addition:

$$\mathrm{\mid }\vec{R}\mathrm{\mid }=\sqrt{s^2+s^2+2s^2\cos {60}^{\circ }}=\sqrt{3s^2}=s\sqrt{3}$$
$$\boxed{{\displaystyle \mathrm{\mid }\vec{R}\mathrm{\mid }=500\sqrt{3}\approx 866\text{ m}}}$$

Path length covered:

$$8\times 500=\boxed{{\displaystyle 4000\text{ m}}}$$

Comparison:

$$\text{Displacement (}\approx 866\text{ m)}<\text{Path length (4000 m)}$$

---

Question 3.11 

A passenger arriving in a new town wishes to go from the station to a hotel located 10 km away on a straight road from the station. A dishonest cabman takes him along a circuitous path 23 km long and reaches the hotel in 28 min. Find:

(a) the average speed of the taxi
(b) the magnitude of average velocity
Are the two equal?

---

Given

• Straight-line distance (displacement) = 10 km

• Actual path length = 23 km

• Time taken = 28 min = ${\displaystyle \frac{28}{60}}={\displaystyle \frac{7}{15}}$

---

(a) Average speed

$$\text{Average speed}=\frac{\text{total distance}}{\text{time}}=\frac{23}{7\mathrm{/}15}=\frac{23\times 15}{7}$$

$$\boxed{{\displaystyle \text{Average speed}\approx 49.3{\text{km h}}^{-1}}}$$

---

(b) Magnitude of average velocity

$$\text{Magnitude of average velocity}=\frac{\text{displacement}}{\text{time}}=\frac{10}{7\mathrm{/}15}=\frac{150}{7}$$

$$\boxed{{\displaystyle \mathrm{\mid }\text{Average velocity}\mathrm{\mid }\approx 21.4{\text{km h}}^{-1}}}$$

---

Are the two equal?

❌ No

Reason:

• Average speed depends on total path length

• Average velocity depends on displacement only

Since the path taken is longer than the straight-line distance,

$$\text{Average speed}>\mathrm{\mid }\text{Average velocity}\mathrm{\mid }$$

---

Question 3.12

The ceiling of a long hall is 25 m high. What is the maximum horizontal distance that a ball thrown with a speed of 40 m s⁻¹ can go without hitting the ceiling of the hall?

---

Given

• Speed of projection: $u=40{\text{m s}}^{-1}$

• Maximum allowed height: $H=25\text{m}$

• Acceleration due to gravity: $g=9.8{\text{m s}}^{-2}$

---

Step 1: Condition for not hitting the ceiling

Maximum height of a projectile:

$$H=\frac{u^2{\sin }^2\theta }{2g}$$

For maximum range without touching the ceiling, the ball must just reach the ceiling:

$$25=\frac{(40{)}^2{\sin }^2\theta }{2\times 9.8}$$

$$25=\frac{1600{\sin }^2\theta }{19.6}$$

$${\sin }^2\theta =\frac{25\times 19.6}{1600}=0.30625$$

$$\sin \theta =0.553$$

---

Step 2: Horizontal range

Horizontal range:

$$R=\frac{u^2\sin 2\theta }{g}$$First find $\sin 2\theta$:

$$\sin 2\theta =2\sin \theta \cos \theta =2(0.553)\sqrt{1-{0.553}^2}$$

$$\cos \theta =\sqrt{1-0.30625}=0.833$$

$$\sin 2\theta =2(0.553)(0.833)\approx 0.921$$

Now range:$$R=\frac{1600\times 0.921}{9.8}\approx 150.4\text{m}$$

---

Question 3.13 

A cricketer can throw a ball to a maximum horizontal distance of 100 m. How much high above the ground can the cricketer throw the same ball?

---

Concept used

• Maximum horizontal range:

$$R_{\max }=\frac{u^2}{g}$$

• Maximum height (when thrown vertically upward with same speed):

$$H_{\max }=\frac{u^2}{2g}$$

---

Step 1: Find the speed of projection

Given:$$R_{\max }=100\text{m}$$
$$\frac{u^2}{g}=100\Rightarrow u^2=100g$$

---

Step 2: Find the maximum height

$$H_{\max }=\frac{u^2}{2g}=\frac{100g}{2g}=50\text{m}$$

---

Question 3.14 

A stone tied to the end of a string 80 cm long is whirled in a horizontal circle with a constant speed. If the stone makes 14 revolutions in 25 s, find the magnitude and direction of the acceleration of the stone.

---

Given

• Radius of circular path:

  $$R=80\text{ cm}=0.8\text{ m}$$

• Number of revolutions: $n=14$

• Time taken: $t=25\text{ s}$

---

Step 1: Find angular speed

$$\omega =\frac{2\pi n}{t}=\frac{2\pi \times 14}{25}=\frac{28\pi }{25}\approx 3.52{\text{rad s}}^{-1}$$

---

Step 2: Find centripetal acceleration

For uniform circular motion,

$$a={\omega }^{2}R$$
$$a=(3.52{)}^2\times 0.8\approx 12.38\times 0.8\approx 9.9{\text{m s}}^{-2}$$

---

Direction of acceleration

• The acceleration is centripetal, i.e.

• always directed towards the centre of the circular path, radially inward.

---

Question 3.15 

An aircraft executes a horizontal loop of radius 1.00 km with a steady speed of 900 km h⁻¹. Compare its centripetal acceleration with the acceleration due to gravity.

---

Given

• Radius of loop:R

  $$=1.00\text{ km}=1000\text{ m}$$

• Speed of aircraft:

  $$v=900{\text{km h}}^{-1}=\frac{900\times 1000}{3600}=250{\text{m s}}^{-1}$$

• Acceleration due to gravity:

  $$g=9.8{\text{m s}}^{-2}$$

---

Centripetal acceleration

$$a_c=\frac{v^2}{R}=\frac{(250{)}^2}{1000}=\frac{62500}{1000}=62.5{\text{m s}}^{-2}$$

---

Comparison with gravity

$$\frac{a_c}{g}=\frac{62.5}{9.8}\approx 6.4$$

---

Question 3.16 

Read each statement below carefully and state, with reasons, whether it is true or false :

---

(a) The net acceleration of a particle in circular motion is always along the radius of the circle towards the centre

❌ False

Reason:

• In uniform circular motion, the net acceleration is centripetal, directed towards the centre.

• But in non-uniform circular motion, there is also a tangential acceleration due to change in speed.

• Hence the net acceleration is not always purely radial.

---

(b) The velocity vector of a particle at a point is always along the tangent to the path of the particle at that point

✅ True

Reason:
Velocity is the time rate of change of position, and in the limit $\mathrm{\Delta }t\to 0$, the displacement is along the tangent to the path. Hence instantaneous velocity is tangential.

---

(c) The acceleration vector of a particle in uniform circular motion averaged over one cycle is a null vector

✅ True

Reason:
In uniform circular motion:

• The magnitude of centripetal acceleration is constant,

• But its direction continuously changes and covers all directions in one complete cycle.

• The vector sum (and hence average) of acceleration over one full cycle is zero.

---

Question 3.17 

The position of a particle is given by

$$\vec{r}(t)=(3.0t^2)\widehat{i}-(2.0t)\widehat{j}+(4.0)\widehat{k}\text{ m}$$

where $t$ is in seconds.

(a) Find the velocity $\vec{v}$ and acceleration $\vec{a}$ of the particle.
(b) Find the magnitude and direction of the velocity at $t=2.0\text{ s}$.

---

(a) Velocity and acceleration

Velocity is the time derivative of position:

$$\vec{v}=\frac{d\vec{r}}{dt}=(6.0t)\widehat{i}-(2.0)\widehat{j}+0\widehat{k}$$

$$\boxed{{\displaystyle \vec{v}(t)=(6.0t)\widehat{i}-2.0\widehat{j}{\text{m s}}^{-1}}}$$

Acceleration is the time derivative of velocity:

$$\vec{a}=\frac{d\vec{v}}{dt}=6.0\widehat{i}$$

$$\boxed{{\displaystyle \vec{a}=6.0\widehat{i}{\text{m s}}^{-2}}}$$

---

(b) Velocity at $t=2.0\text{ s}$

Substitute $t=2.0$ s in $\vec{v}(t)$:

$$\vec{v}(2)=(12)\widehat{i}-2\widehat{j}{\text{m s}}^{-1}$$

Magnitude

$$\mathrm{\mid }\vec{v}\mathrm{\mid }=\sqrt{{12}^2+(-2{)}^2}=\sqrt{148}\approx \boxed{{\displaystyle 12.2{\text{m s}}^{-1}}}$$

Direction

Angle $\theta$ with the positive $x$-axis:

$$\tan \theta =\frac{\mathrm{\mid }{v}_y\mathrm{\mid }}{v_x}=\frac{2}{12}=\frac{1}{6}\Rightarrow \theta \approx {9.5}^{\circ }$$

Since $v_x>0$ and $v_y<0$, the direction is below the +x-axis.

$$\boxed{{\displaystyle \text{Direction: }{9.5}^{\circ }\text{ below the positive }x\text{-axis}}}$$

---

Question 3.18 

A particle starts from the origin at $t=0\text{ s}$ with a velocity

$${\vec{v}}_0=10.0\widehat{j}{\text{m s}}^{-1}$$

and moves in the x–y plane with a constant acceleration

$$\vec{a}=(8.0\widehat{i}+2.0\widehat{j}){\text{m s}}^{-2}\mathrm{.}$$

(a) At what time is the x-coordinate of the particle 16 m? What is the y-coordinate at that time?
(b) What is the speed of the particle at that time?

---

Given

• Initial position: $x_0=0,y_0=0$

• Initial velocity components:
  $u_x=0,u_y=10.0{\text{m s}}^{-1}$

• Acceleration components:
  $a_x=8.0,a_y=2.0{\text{m s}}^{-2}$

---

(a) Time when $x=16\text{ m}$ and corresponding $y$

x–motion:

$$x=u_{x}t+\frac{1}{2}{a}_x{t}^2=0+\frac{1}{2}(8.0)t^2=4t^2$$

Set $x=16$:

$$4t^2=16\Rightarrow t^2=4\Rightarrow \boxed{{\displaystyle t=2.0\text{ s}}}$$

y–motion at $t=2.0\text{ s}$:

$$y=u_{y}t+\frac{1}{2}{a}_y{t}^2=10(2)+\frac{1}{2}(2)(2^2)=20+4=\boxed{{\displaystyle 24\text{ m}}}$$

---

(b) Speed at $t=2.0\text{ s}$

Velocity components at time $t$:

$$v_x=u_x+a_{x}t=0+8(2)=16{\text{m s}}^{-1}$$

$$v_y=u_y+a_{y}t=10+2(2)=14{\text{m s}}^{-1}$$

Speed:

$$v=\sqrt{v_x^2+v_y^2}=\sqrt{{16}^2+{14}^2}=\sqrt{452}\approx \boxed{{\displaystyle 21.3{\text{m s}}^{-1}}}$$

---

Question 3.19 

$\widehat{i}$ and $\widehat{j}$ are unit vectors along the x-axis and y-axis respectively.

(a) What are the magnitude and direction of the vectors

$$(\widehat{i}+\widehat{j})\text{and}(\widehat{i}-\widehat{j})?$$

(b) What are the components of a vector

$$\vec{A}=2\widehat{i}+3\stackrel{^<span\; style="font-size:\; var(--wp--preset--font-size--x-large);\; letter-spacing:\; -0.1px;\; font-family:\; var(--wp--preset--font-family--manrope);"></span>}{j}$$

along the directions of $(\widehat{i}+\widehat{j})$ and $(\widehat{i}-\widehat{j})$?
(Graphical method may be used.)

---

(a) Magnitude and direction

Vector $\widehat{i}+\widehat{j}$

Magnitude

$$\mathrm{\mid }\widehat{i}+\widehat{j}\mathrm{\mid }=\sqrt{1^2+1^2}=\sqrt{2}$$

Direction

$$\tan \theta =\frac{1}{1}=1\Rightarrow \theta ={45}^{\circ }$$

➡️ Direction: 45° above the +x-axis

---

Vector $\widehat{i}-\widehat{j}$

Magnitude

$$\mathrm{\mid }\widehat{i}-\widehat{j}\mathrm{\mid }=\sqrt{1^2+(-1{)}^2}=\sqrt{2}$$

Direction

$$\tan \theta =\frac{-1}{1}=-1\Rightarrow \theta =-{45}^{\circ }$$

➡️ Direction: 45° below the +x-axis

---

(b) Components of $\vec{A}=2\widehat{i}+3\widehat{j}$

First find unit vectors along the given directions.

Unit vector along $(\widehat{i}+\widehat{j})$

$${\widehat{n}}_1=\frac{\widehat{i}+\widehat{j}}{\sqrt{2}}$$

Unit vector along $(\widehat{i}-\widehat{j})$

$${\widehat{n}}_2=\frac{\widehat{i}-\widehat{j}}{\sqrt{2}}$$

---

Component of $\vec{A}$ along $(\widehat{i}+\widehat{j})$

$$A_1=\vec{A}\cdot {\widehat{n}}_1=\frac{1}{\sqrt{2}}(2+3)=\frac{5}{\sqrt{2}}$$

---

Component of $\vec{A}$ along $(\widehat{i}-\widehat{j})$

$$A_2=\vec{A}\cdot {\widehat{n}}_2=\frac{1}{\sqrt{2}}(2-3)=-\frac{1}{\sqrt{2}}$$

---

Question 3.20 

For any arbitrary motion in space, which of the following relations are true? Give reasons.

---

(a)

$${\vec{v}}_{\text{average}}=\frac{1}{2}[\vec{v}(t_1)+\vec{v}(t_2)]$$

❌ False

Reason:
This relation holds only for motion with constant acceleration.
For arbitrary (general) motion, velocity need not vary linearly with time.

---

(b)

$${\vec{v}}_{\text{average}}=\frac{\vec{r}(t_2)-\vec{r}(t_1)}{t_2-t_1}$$

✅ True

Reason:
This is the definition of average velocity, valid for all kinds of motion.

---

(c)

$$\vec{v}(t)=\vec{v}(0)+\vec{a}t$$

❌ False

Reason:
This equation is valid only when acceleration is constant.
For arbitrary motion, acceleration may vary with time.

---

(d)

$$\vec{r}(t)=\vec{r}(0)+\vec{v}(0)t+\frac{1}{2}\vec{a}{t}^2$$

❌ False

Reason:
This is a kinematic equation applicable only for constant acceleration.
Not valid for arbitrary motion.

---

(e)

$${\vec{a}}_{\text{average}}=\frac{\vec{v}(t_2)-\vec{v}(t_1)}{t_2-t_1}$$

✅ True

Reason:
This is the definition of average acceleration, valid for any motion.

---

Question 3.21 

Read each statement below carefully and state, with reasons and examples, whether it is true or false:

A scalar quantity is one that—

---

(a) is conserved in a process

❌ False

Reason:
Being a scalar does not imply conservation. Conservation depends on physical laws, not on whether a quantity is scalar or vector.

Example:

• Energy (scalar) is conserved (in isolated systems).

• Temperature (scalar) is not conserved.

---

(b) can never take negative values

❌ False

Reason:
Scalars can be positive, negative, or zero.

Example:

• Temperature on the Celsius scale can be negative.

• Electric potential can be negative.

---

(c) must be dimensionless

❌ False

Reason:
Most scalars have dimensions and units.

Example:

• Mass (kg), time (s), energy (J) are scalars with dimensions.

• Only some scalars (e.g., coefficient of friction) are dimensionless.

---

(d) does not vary from one point to another in space

❌ False

Reason:
A scalar quantity may vary from point to point, forming a scalar field.

Example:

• Temperature varies from place to place in a room.

• Pressure varies with depth in a fluid.

---

(e) has the same value for observers with different orientations of axes

✅ True

Reason:
Scalars are independent of the choice of coordinate axes and their orientation.

Example:

• Mass, time, temperature remain the same regardless of how axes are oriented.

---

---

Question 3.22 

An aircraft is flying at a height of 3400 m above the ground. If the angle subtended at a ground observation point by the aircraft positions 10.0 s apart is ${30}^{\circ }$, what is the speed of the aircraft?

---

Understanding the situation

• The aircraft flies horizontally at a constant height.

• From a fixed point on the ground, the lines of sight to the aircraft at two positions (separated by 10 s) make an angle of 30° with each other.

• Height of aircraft:

$$h=3400\text{ m}$$

For maximum clarity (and as done in NCERT), we assume the aircraft is observed before and after it passes the point of closest approach, so the two angles with the vertical are symmetric.

Hence, each angle with the vertical:

$$\theta =\frac{{30}^{\circ }}{2}={15}^{\circ }$$

---

Horizontal distance covered in 10 s

Let the horizontal distance from the observer to each position be $x$.

From right-angled triangle:

$$\tan {15}^{\circ }=\frac{x}{3400}$$
$$x=3400\tan {15}^{\circ }$$

Using $\tan {15}^{\circ }\approx 0.268$:

$$x\approx 3400\times 0.268\approx 911\text{ m}$$

So, total horizontal distance travelled in 10 s:

$$\text{Distance}=2x\approx 2\times 911=1822\text{ m}$$

---

Speed of the aircraft

$$v=\frac{\text{distance}}{\text{time}}=\frac{1822}{10}\approx 182{\text{m s}}^{-1}$$

---