Class 11th Physics Chapter-6 Solutions

Question 6.1

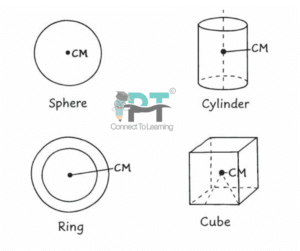
Give the location of the centre of mass of a (i) sphere, (ii) cylinder, (iii) ring, and (iv) cube, each of uniform mass density. Does the centre of mass of a body necessarily lie inside the body ?

Answer:

For bodies having uniform mass density, the centre of mass coincides with their geometric centre due to symmetry.

1. Sphere:
   The centre of mass lies at the geometric centre of the sphere.

2. Cylinder:
   The centre of mass lies at the midpoint of its axis, i.e., the geometric centre of the cylinder.

3. Ring:
   The centre of mass lies at the centre of the ring (centre of the circular shape), even though there is no material present at that point.

4. Cube:
   The centre of mass lies at the geometric centre of the cube (intersection of its body diagonals).

---

Question 6.2

In the HCl molecule, the separation between the nuclei of the two atoms is about 1.27 Å (1 Å = 10⁻¹⁰ m). Find the approximate location of the centre of mass (CM) of the molecule, given that a chlorine atom is about 35.5 times as massive as a hydrogen atom and nearly all the mass of an atom is concentrated in its nucleus.

Answer:

Let the hydrogen nucleus (H) be at the origin.

• Mass of hydrogen nucleus = $m$

• Mass of chlorine nucleus = $35.5m$

• Distance between H and Cl nuclei = $1.27\mathring{\text{A}}$

So,

• Position of H nucleus: $x_1=0$

• Position of Cl nucleus: $x_2=1.27\mathring{\text{A}}$

The centre of mass is given by:

$$x_{\text{CM}}=\frac{m_1{x}_1+m_2{x}_2}{m_1+m_2}$$

Substitute values:

$$x_{\text{CM}}=\frac{m(0)+35.5m(1.27)}{m+35.5m}$$

$$\frac{\mathrm{<span\; style="font-size:\; revert;\; font-family:\; var(--wp--preset--font-family--manrope);\; letter-spacing:\; -0.1px;"></span>}}{}$$$$x_{\text{CM}}=\frac{35.5\times 1.27}{36.5}$$

$$x_{\text{CM}}\approx 1.24\mathring{\text{A}}$$

---

Question 6.3

A child sits stationary at one end of a long trolley moving uniformly with a speed $V$ on a smooth horizontal floor. If the child gets up and runs about on the trolley in any manner, what is the speed of the centre of mass (CM) of the (trolley + child) system?

---

Answer :

Since the trolley is moving on a smooth horizontal floor, there is no external horizontal force acting on the trolley + child system.

According to the law of conservation of linear momentum:

If no external force acts on a system, the velocity of its centre of mass remains constant.

Initially, the entire system (trolley + child) is moving with speed $V$.
When the child runs about on the trolley, all the forces involved are internal forces between the child and the trolley.

Internal forces cannot change the motion of the centre of mass.

Final Answer

$$\boxed{{\displaystyle \text{The speed of the centre of mass remains }V\mathrm{.}}}$$

---

Question 6.4

Show that the area of the triangle contained between the vectors a and b is one half of the magnitude of a × b.

---

Proof :

Let a and b be two vectors with an angle θ between them.

Step 1: Area using basic geometry

The area of a triangle formed by two sides a and b with included angle θ is:

$$\text{Area of triangle}=\frac{1}{2}ab\sin \theta$$

Step 2: Magnitude of vector product

By definition of the vector (cross) product:

$$\mathrm{\mid }\mathbf{a}\times \mathbf{b}\mathrm{\mid }=ab\sin \theta$$

Step 3: Compare the two results

From above,$$\text{Area of triangle}=\frac{1}{2}\mathrm{\mid }\mathbf{a}\times \mathbf{b}\mathrm{\mid }$$

---

Question 6.5

Show that $\mathbf{a}\cdot (\mathbf{b}\times \mathbf{c})$ is equal in magnitude to the volume of the parallelepiped formed on the three vectors $\mathbf{a},\mathbf{b}$and $\mathbf{c}$.

---

Proof :

Consider a parallelepiped formed by the three vectors
$\mathbf{a},\mathbf{b}$ and $\mathbf{c}$.

Step 1: Area of the base

The base of the parallelepiped is the parallelogram formed by vectors
$\mathbf{b}$ and $\mathbf{c}$.

The area of this base is given by the magnitude of their vector product:

$$\text{Area of base}=\mathrm{\mid }\mathbf{b}\times \mathbf{c}\mathrm{\mid }$$

Step 2: Height of the parallelepiped

Let θ be the angle between vector $\mathbf{a}$ and the vector $\mathbf{b}\times \mathbf{c}$.

The height (h) of the parallelepiped is the component of $\mathbf{a}$ along the direction perpendicular to the base:

$$h=\mathrm{\mid }\mathbf{a}\mathrm{\mid }\cos \theta$$

Step 3: Volume of the parallelepiped

$$\text{Volume}=(\text{Area of base})\times (\text{Height})$$

$$\text{Volume}=\mathrm{\mid }\mathbf{b}\times \mathbf{c}\mathrm{\mid }\mathrm{\mid }\mathbf{a}\mathrm{\mid }\cos \theta$$

Step 4: Use scalar triple product

By definition of the scalar (triple) product:

$$\mathbf{a}\cdot (\mathbf{b}\times \mathbf{c})=\mathrm{\mid }\mathbf{a}\mathrm{\mid }\mathrm{\mid }\mathbf{b}\times \mathbf{c}\mathrm{\mid }\cos \theta$$

---

Question 6.6

Find the components along the x, y and z axes of the angular momentum l of a particle whose position vector is r with components (x, y, z) and momentum p with components $(p_x,p_y,p_z)$. Show that if the particle moves only in the x–y plane, the angular momentum has only a z-component.

---

Solution :

The angular momentum of a particle is defined as:

$$\mathbf{l}=\mathbf{r}\times \mathbf{p}$$

Step 1: Write vectors in component form

$$\mathbf{r}=x\widehat{i}+y\widehat{j}+z\widehat{k}$$

$$\mathbf{p}=p_x\widehat{i}+p_y\widehat{j}+p_z\widehat{k}$$

Step 2: Find the cross product using determinant

$$\mathbf{l}=\mid \begin{array}{ccc}\widehat{i}& \widehat{j}& \widehat{k}\\ x& y& z\\ p_x& p_y& p_z\end{array}\mid$$

Expanding:

$$\mathbf{l}=\widehat{i}(y{p}_z-z{p}_y)-\widehat{j}(x{p}_z-z{p}_x)+\widehat{k}(x{p}_y-y{p}_x)$$

Step 3: Components of angular momentum

$$l_x=y{p}_z-z{p}_y$$

$$l_y=z{p}_x-x{p}_z$$

$$l_z=x{p}_y-y{p}_x$$

Step 4: Particle moving only in the x–y plane

For motion in the x–y plane:

$$z=0\text{and}{p}_z=0$$

Substitute into the components:

$$l_x=y(0)-0(p_y)=0$$

$$l_y=0(p_x)-x(0)=0$$

$$l_z=x{p}_y-y{p}_x\mathrm{\ne }0$$

---

Question 6.7

Two particles, each of mass $m$ and speed $v$, travel in opposite directions along parallel lines separated by a distance $d$. Show that the angular momentum vector of the two-particle system is the same whatever be the point about which the angular momentum is taken.

---

Solution :

Let the two particles move along parallel straight lines, separated by a perpendicular distance $d$.

• Mass of each particle = $m$

• Speed of each particle = $v$

• Momenta:

  $${\mathbf{p}}_1=m\mathbf{v},{\mathbf{p}}_2=-m\mathbf{v}$$

Step 1: Choose any arbitrary origin O

Let the perpendicular distances of the two lines of motion from O be $r_1$ and $r_2$, such that:

$$r_1+r_2=d$$

Step 2: Angular momentum of each particle

Angular momentum magnitude of a particle moving in a straight line:

$$L=(\text{momentum})\times (\text{perpendicular distance})$$

For particle 1:

$$L_1=mv{r}_1$$

For particle 2:

$$L_2=mv{r}_2$$

Step 3: Total angular momentum of the system

Both angular momentum vectors point in the same direction (given by the right-hand rule), so they add:

$$L_{\text{total}}=L_1+L_2=mv(r_1+r_2)$$

$$L_{\text{total}}=mvd$$

Step 4: Independence from choice of origin

The result depends only on $d$ (the separation between the lines) and not on $r_1$ or $r_2$ individually.

Hence, no matter where the origin is chosen, the total angular momentum remains the same.

---

Question 6.8

A non-uniform bar of weight $W$ is suspended at rest by two strings of negligible weight as shown in Fig. 6.33. The angles made by the strings with the vertical are ${36.9}^{\circ }$ and ${53.1}^{\circ }$respectively. The bar is 2 m long. Calculate the distance $d$ of the centre of gravity of the bar from its left end.

---

Solution :

Let the tensions in the left and right strings be $T_1$ and $T_2$ respectively.

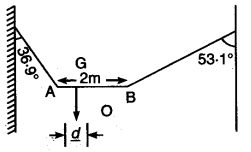
Given:

$$\sin {36.9}^{\circ }=0.6,\cos {36.9}^{\circ }=0.8$$

$$\sin {53.1}^{\circ }=0.8,\cos {53.1}^{\circ }=0.6$$

---

Step 1: Horizontal equilibrium

Since the bar is at rest, horizontal components must balance:

$$T_1\sin {36.9}^{\circ }=T_2\sin {53.1}^{\circ }$$

$$T_1(0.6)=T_2(0.8)$$

$$T_1=\frac{4}{3}{T}_2$$

Step 2: Vertical equilibrium

Sum of vertical components equals weight $W$:

$$T_1\cos {36.9}^{\circ }+T_2\cos {53.1}^{\circ }=W$$

$$\frac{4}{3}{T}_2(0.8)+T_2(0.6)=W$$

$$(1.0667+0.6)T_2=W$$

$$T_2=0.6W,T_1=0.8W$$

Step 3: Take moments about the left end

• Vertical component of $T_1$ acts at the left end → no moment

• Vertical component of $T_2$:

$$T_2\cos {53.1}^{\circ }=0.6W\times 0.6=0.36W$$Taking moments about the left end:

$$(0.36W)(2)=W\cdot d$$

$$d=0.72\text{ m}$$

---

Question 6.9

A car weighs 1800 kg. The distance between its front and back axles is 1.8 m. Its centre of gravity is 1.05 m behind the front axle. Determine the force exerted by the level ground on each front wheel and each back wheel.

---

Given

• Mass of car, $m=1800\text{kg}$

• Weight of car,

  $$W=mg=1800\times 9.8=17640\text{N}$$

• Distance between axles = $1.8\text{m}$

• Distance of centre of gravity from front axle = $1.05\text{m}$

So, distance of CG from rear axle:

$$1.8-1.05=0.75\text{m}$$

---

Step 1: Let reactions be

• Reaction at front axle = $R_f$

• Reaction at rear axle = $R_r$

---

Step 2: Vertical equilibrium

$$R_f+R_r=W=17640$$

---

Step 3: Take moments about the front axle

Moment due to rear reaction = moment due to weight

$$R_r\times 1.8=17640\times 1.05$$

$$R_r=\frac{17640\times 1.05}{1.8}$$

$$R_r=10290\text{N}$$

---

Step 4: Find reaction at front axle

$$R_f=17640-10290=7350\text{N}$$

Step 5: Force on each wheel

Each axle has two wheels.

• Force on each back wheel:

$$\frac{R_r}{2}=\frac{10290}{2}=5145\text{N}$$

• Force on each front wheel:

$$\frac{R_f}{2}=\frac{7350}{2}=3675\text{N}$$

---

Question 6.10

Torques of equal magnitude are applied to a hollow cylinder and a solid sphere, both having the same mass and radius. The cylinder is free to rotate about its standard axis of symmetry, and the sphere is free to rotate about an axis passing through its centre. Which of the two will acquire a greater angular speed after a given time?

---

Solution :

Given:

• Same torque $\tau$

• Same mass $M$

• Same radius $R$

• Same time of application

Angular acceleration is given by:

$$\alpha =\frac{\tau }{I}$$

where $I$ is the moment of inertia.

---

Step 1: Moments of inertia

• Hollow cylinder (about its symmetry axis):

$$I_{\text{cyl}}=M{R}^2$$

• Solid sphere (about diameter):

$$I_{\text{sphere}}=\frac{2}{5}M{R}^2$$

---

Step 2: Compare angular accelerations

$${\alpha }_{\text{cyl}}=\frac{\tau }{M{R}^2}$$

$${\alpha }_{\text{sphere}}=\frac{\tau }{\frac{2}{5}M{R}^2}=\frac{5\tau }{2M{R}^2}$$

Clearly,

$${\alpha }_{\text{sphere}}>{\alpha }_{\text{cyl}}$$

Step 3: Angular speed after given time

Angular speed acquired after time $t$:

$$\omega =\alpha t$$

Since both start from rest and torque acts for the same time:

$${\omega }_{\text{sphere}}>{\omega }_{\text{cyl}}$$

---

Question 6.11

A solid cylinder of mass 20 kg rotates about its axis with angular speed $100{\text{rad s}}^{-1}$
The radius of the cylinder is 0.25 m.
(i) What is the kinetic energy associated with the rotation of the cylinder?
(ii) What is the magnitude of angular momentum of the cylinder about its axis?

---

Given

• Mass, $M=20\text{kg}$

• Radius, $R=0.25\text{m}$

• Angular speed, $\omega =100{\text{rad s}}^{-1}$

For a solid cylinder about its axis:

$$I=\frac{1}{2}M{R}^2$$

Step 1: Moment of inertia

$$I=\frac{1}{2}(20)(0.25{)}^2=10\times 0.0625=0.625{\text{kg m}}^2$$

(i) Rotational kinetic energy

$$K=\frac{1}{2}I{\omega }^2$$

$$K=\frac{1}{2}(0.625)(100{)}^2$$

$$K=0.3125\times 10000=3125\text{J}$$

(ii) Angular momentum

$$L=I\omega$$

$$L=0.625\times 100=62.5{\text{kg m}}^2{\text{s}}^{-1}$$

---

Question 6.12

(a) A child stands at the centre of a turntable with his two arms outstretched. The turntable is set rotating with an angular speed of 40 rev/min. How much is the angular speed of the child if he folds his hands back and thereby reduces his moment of inertia to $\frac{2}{5}$ times the initial value? Assume that the turntable rotates without friction.

(b) Show that the child’s new kinetic energy of rotation is more than the initial kinetic energy of rotation. How do you account for this increase in kinetic energy?

---

Solution

(a) New angular speed

Since the turntable rotates without friction, there is no external torque on the system (child + turntable).

Hence, angular momentum is conserved.

$$I_1{\omega }_1=I_2{\omega }_2$$

Given:

$${\omega }_1=40\text{rev/min}$$

$$I_2=\frac{2}{5}{I}_1$$

Substitute:

$$I_1(40)=\frac{2}{5}{I}_1{\omega }_2$$

Cancel $I_1$:

$$40=\frac{2}{5}{\omega }_2$$

$${\omega }_2=40\times \frac{5}{2}=100\text{rev/min}$$

Answer (a)

$$\boxed{{\displaystyle {\omega }_2=100\text{rev/min}}}$$

(b) Change in kinetic energy

Rotational kinetic energy:

$$K=\frac{1}{2}I{\omega }^2$$

Initial kinetic energy

$$K_1=\frac{1}{2}{I}_1{\omega }_1^2$$

Final kinetic energy

$$K_2=\frac{1}{2}{I}_2{\omega }_2^2$$

Substitute $I_2=\frac{2}{5}{I}_1$ and ${\omega }_2=\frac{5}{2}{\omega }_1$:

$$K_2=\frac{1}{2}\left(\frac{2}{5}{I}_1\right){\left(\frac{5}{2}{\omega }_1\right)}^2$$

$$K_2=\frac{1}{2}{I}_1{\omega }_1^2\times \frac{25}{10}$$

$$K_2=\frac{5}{2}{K}_1$$

Conclusion (b)

$$\boxed{{\displaystyle K_2>K_1}}$$

The kinetic energy of rotation increases when the child folds his arms.

Explanation for increase in kinetic energy

The increase in kinetic energy comes from the work done by the child while pulling his arms inward against centrifugal effects.
This work is converted into rotational kinetic energy.

---

Question 6.13

A rope of negligible mass is wound round a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N? What is the linear acceleration of the rope? Assume that there is no slipping.

---

Given

• Mass of hollow cylinder, $M=3\text{kg}$

• Radius, $R=40\text{cm}=0.40\text{m}$

• Pulling force, $F=30\text{N}$

For a hollow cylinder about its axis:

$$I=M{R}^2$$

Step 1: Torque on the cylinder

The force applied on the rope produces a torque:

$$\tau =FR=30\times 0.40=12\text{N m}$$

Step 2: Angular acceleration

Using rotational equation of motion:

$$\tau =I\alpha$$

$$12=(M{R}^2)\alpha$$

$$12=(3)(0.40{)}^2\alpha$$

$$12=3\times 0.16\alpha =0.48\alpha$$

$$\alpha =\frac{12}{0.48}=25{\text{rad s}}^{-2}$$

Angular acceleration

$$\boxed{{\displaystyle \alpha =25{\text{rad s}}^{-2}}}$$

Step 3: Linear acceleration of the rope

Since there is no slipping:

$$a=\alpha R$$
$$a=25\times 0.40=10{\text{m s}}^{-2}$$

Linear acceleration of the rope

$$\boxed{{\displaystyle a=10{\text{m s}}^{-2}}}$$

---

Question 6.14

To maintain a rotor at a uniform angular speed of $200{\text{rad s}}^{-1}$, an engine needs to transmit a torque of $180\text{N m}$. What is the power required by the engine?
(Note: uniform angular velocity in the absence of friction implies zero torque. In practice, applied torque is needed to counter frictional torque). Assume that the engine is 100% efficient.

---

Solution :

Given:

• Angular speed, $\omega =200{\text{rad s}}^{-1}$

• Torque, $\tau =180\text{N m}$

The power delivered by a rotating engine is given by:

$$P=\tau \omega$$

Substitute the given values:

$$P=180\times 200$$
$$P=36000\text{W}$$

---

Question 6.15

From a uniform disc of radius $R$, a circular hole of radius $R\mathrm{/}2$ is cut out. The centre of the hole is at a distance $R\mathrm{/}2$from the centre of the original disc. Locate the centre of gravity of the resulting flat body.

---

Solution :

Step 1: Use method of superposition

Treat the removed hole as a negative mass.

Let:

• Surface mass density = $\sigma$ (uniform)

• Mass of full disc:

$$M=\sigma \pi R^2$$

• Mass of removed disc (hole):

$$m=\sigma \pi {\left(\frac{R}{2}\right)}^2=\frac{1}{4}M$$

Step 2: Choose coordinate system

• Take the centre of the original disc as origin $O$

• Let the centre of the hole be along the +x-axis at distance $R\mathrm{/}2$

So:

• Position of full disc CM: $x_1=0$

• Position of hole CM: $x_2=R\mathrm{/}2$

---

Step 3: Centre of mass formula

$$x_{\text{CM}}=\frac{M{x}_1-m{x}_2}{M-m}$$

(Subtract because the hole represents negative mass.)

Substitute values:

$$x_{\text{CM}}=\frac{M(0)-\frac{1}{4}M\left(\frac{R}{2}\right)}{M-\frac{1}{4}M}$$

$$x_{\text{CM}}=\frac{-\frac{MR}{8}}{\frac{3M}{4}}$$

$$x_{\text{CM}}=-\frac{R}{6}$$

---

Question 6.16

A metre stick is balanced on a knife edge at its centre. When two coins, each of mass 5 g, are put one on top of the other at the 12.0 cm mark, the stick is found to be balanced at 45.0 cm. What is the mass of the metre stick?

---

Solution :

Given

• Length of metre stick = 100 cm

• Initial balance point (centre of stick) = 50 cm

• New balance point = 45 cm

• Mass of each coin = 5 g

• Total mass of coins = $10\text{g}$

• Position of coins = 12 

Let the mass of the metre stick be $M$ grams.

Principle Used

For equilibrium about the knife edge,

$$\text{Sum of clockwise moments}=\text{Sum of anticlockwise moments}$$

Step 1: Distances from the new balance point (45 cm)

• Distance of coins from knife edge:

$$45-12=33\text{cm}$$

• Distance of stick’s centre of gravity from knife edge:

$$50-45=5\text{cm}$$

Step 2: Take moments about the knife edge

Moment due to coins = Moment due to metre stick

$$(10)(33)=M(5)$$

Step 3: Solve for $M$

$$M=\frac{10\times 33}{5}=66\text{g}$$

---

Question 6.17

The oxygen molecule has a mass of $5.30\times {10}^{-26}\text{kg}$and a moment of inertia of   
$1.94\times {10}^{-46}{\text{kg m}}^2$about an axis through its centre perpendicular to the line joining the two atoms. Suppose the mean speed of such a molecule in a gas is $500{\text{m s}}^{-1}$ and that its kinetic energy of rotation is two thirds of its kinetic energy of translation. Find the average angular velocity of the molecule.

---

Solution :

Given

• Mass of molecule,

  $$m=5.30\times {10}^{-26}\text{kg}$$

• Moment of inertia,

  $$I=1.94\times {10}^{-46}{\text{kg m}}^2$$

• Mean speed,

  $$v=500{\text{m s}}^{-1}$$

• Rotational KE $=\frac{2}{3}$ of translational KE

---

Step 1: Translational kinetic energy

$$K_{\text{trans}}=\frac{1}{2}m{v}^2$$

$$K_{\text{trans}}=\frac{1}{2}(5.30\times {10}^{-26})(500{)}^2$$

$$K_{\text{trans}}=\frac{1}{2}(5.30\times {10}^{-26})(2.5\times {10}^5)$$

$$K_{\text{trans}}=6.63\times {10}^{-21}\text{J}$$

Step 2: Rotational kinetic energy

$$K_{\text{rot}}=\frac{2}{3}{K}_{\text{trans}}$$$$K_{\text{rot}}=\frac{2}{3}(6.63\times {10}^{-21})=4.42\times {10}^{-21}\text{J}$$

Step 3: Use rotational KE formula

$$K_{\text{rot}}=\frac{1}{2}I{\omega }^2$$

$$\frac{1}{2}(1.94\times {10}^{-46}){\omega }^2=4.42\times {10}^{-21}$$

$${\omega }^2=\frac{2(4.42\times {10}^{-21})}{1.94\times {10}^{-46}}$$

$${\omega }^2=4.56\times {10}^{25}$$

$$\omega =\sqrt{4.56\times {10}^{25}}\approx 6.75\times {10}^{12}{\text{rad s}}^{-1}$$