Class 11th Physics Chapter-7 Solutions

Question 7.1

Answer the following:

Question 7.1 (a)

You can shield a charge from electrical forces by putting it inside a hollow conductor.
Can you shield a body from the gravitational influence of nearby matter by putting it inside a hollow sphere or by some other means?

Answer:
No, gravitational shielding is not possible. Although the gravitational force due to a hollow spherical shell on a body inside it is zero, external masses still exert gravitational force on the body. Unlike electric charges, there is no negative mass and no gravitational analogue of a conductor. Hence, gravity cannot be shielded by any means.

---

Question 7.1 (b)

An astronaut inside a small spaceship orbiting around the Earth cannot detect gravity. If the space station orbiting around the Earth has a large size, can he hope to detect gravity?

Answer:
No, even in a large space station the astronaut cannot directly detect gravity because both the astronaut and the station are in free fall under Earth’s gravity. However, in a very large station, extremely small tidal effects (due to variation of gravity from one point to another) may be detectable with sensitive instruments.

---

Question 7.1 (c)

If you compare the gravitational force on the Earth due to the Sun to that due to the Moon, you would find that the Sun’s pull is greater than the Moon’s pull. However, the tidal effect of the Moon’s pull is greater than the tidal effect of the Sun. Why?

Answer:
Tidal effects depend on the variation (difference) of gravitational force across the Earth, which is proportional to mass divided by the cube of distance. Although the Sun is much more massive, it is very far away. The Moon, being much closer to the Earth, produces a larger variation in gravitational pull across the Earth and hence causes stronger tides.

---

Exercise 7.2

Choose the correct alternative 

---

(a) Acceleration due to gravity decreases with increasing altitude.

✔ As altitude increases, the distance from the Earth’s centre increases, so gravitational pull decreases.

---

(b) Acceleration due to gravity decreases with increasing depth

(assuming the Earth to be a sphere of uniform density).

✔ Inside the Earth, only the mass enclosed within the given radius contributes to gravity, so $g$ decreases as depth increases.

---

(c) Acceleration due to gravity is independent of mass of the body.

✔ $g={\displaystyle \frac{GM}{R^2}}$ depends on the mass of the Earth, not on the mass of the falling body.

---

(d) The formula

$$-GMm(\frac{1}{r_2}-\frac{1}{r_1})$$

is more accurate than the formula

$$mg(r_2-r_1)$$

✔ The $mg(r_2-r_1)$ formula is only an approximation valid near the Earth’s surface, whereas the gravitational potential energy formula is exact.

---

Question 7.3

Suppose there existed a planet that went around the Sun twice as fast as the Earth. What would be its orbital size as compared to that of the Earth?

---

Answer:

Using Kepler’s Third Law,

$$T^2\propto R^3$$

Let

• $T_E$ = time period of Earth

• $R_E$ = orbital radius of Earth

The new planet goes twice as fast, so its time period is half:

$$T_P=\frac{T_E}{2}$$

Applying Kepler’s law:

$${\left(\frac{T_P}{T_E}\right)}^2={\left(\frac{R_P}{R_E}\right)}^3$$

$${\left(\frac{1}{2}\right)}^2={\left(\frac{R_P}{R_E}\right)}^3$$

$$\frac{1}{4}={\left(\frac{R_P}{R_E}\right)}^3$$

$$\frac{R_P}{R_E}={\left(\frac{1}{4}\right)}^{1\mathrm{/}3}$$

$$\boxed{{\displaystyle \frac{R_P}{R_E}=\frac{1}{\sqrt[3]{4}}\approx 0.63}}$$

---

Question 7.4

Io, one of the satellites of Jupiter, has an orbital period of 1.769 days and the radius of the orbit is
$4.22\times {10}^8\text{m}$. Show that the mass of Jupiter is about one–thousandth that of the Sun.

---

Answer:

For a satellite moving in a circular orbit, by Kepler’s third law:

$$M=\frac{4{\pi }^2{R}^3}{G{T}^2}$$where
$M$ = mass of Jupiter,
$R=4.22\times {10}^8\text{m}$
$T=1.769\text{days}=1.769\times 24\times 3600\text{s}$
$G=6.67\times {10}^{-11}{\text{N m}}^2{\text{kg}}^{-2}$

---

Step 1: Convert time period into seconds

$$T=1.769\times 24\times 3600\approx 1.53\times {10}^5\text{s}$$

Step 2: Substitute values

$$M_J=\frac{4{\pi }^2(4.22\times {10}^8{)}^3}{6.67\times {10}^{-11}(1.53\times {10}^5{)}^2}$$

$$M_J\approx 1.9\times {10}^{27}\text{kg}$$

Step 3: Compare with mass of the Sun

$$M_{\text{Sun}}\approx 2.0\times {10}^{30}\text{kg}$$

$$\frac{M_J}{M_{\text{Sun}}}=\frac{1.9\times {10}^{27}}{2.0\times {10}^{30}}\approx {10}^{-3}$$

---

Question 7.5

Let us assume that our galaxy consists of $2.5\times {10}^{11}$ stars, each of one solar mass. How long will a star at a distance of 50,000 ly from the galactic centre take to complete one revolution?
Take the diameter of the Milky Way to be ${10}^5$ ly.

---

Answer:

The star revolves around the galactic centre under the gravitational attraction of the mass enclosed within its orbit.

Step 1: Mass of the galaxy

Each star has one solar mass:

$$M_{\odot }=2\times {10}^{30}\text{kg}$$

Total mass of galaxy:

$$M=2.5\times {10}^{11}\times 2\times {10}^{30}=5\times {10}^{41}\text{kg}$$

Step 2: Radius of orbit

Given distance of star from galactic centre:

$$R=\mathrm{50,000}\text{ly}$$

Convert light year to metre:

$$1\text{ly}=9.46\times {10}^{15}\text{m}$$

$$R=5\times {10}^4\times 9.46\times {10}^{15}=4.73\times {10}^{20}\text{m}$$

Step 3: Time period using circular orbit relation

$$T=2\pi \sqrt{\frac{R^3}{GM}}$$

Substitute values:

$$T=2\pi \sqrt{\frac{(4.73\times {10}^{20}{)}^3}{6.67\times {10}^{-11}\times 5\times {10}^{41}}}$$

$$T\approx 3.5\times {10}^{15}\text{s}$$

Step 4: Convert seconds to years

$$1\text{year}=3.15\times {10}^7\text{s}$$

$$T=\frac{3.5\times {10}^{15}}{3.15\times {10}^7}\approx 1.1\times {10}^8\text{years}$$

---

Exercise 7.6

Choose the correct alternative

---

(a)

If the zero of potential energy is at infinity, the total energy of an orbiting satellite is the negative of its kinetic energy.

✔ For a satellite in circular orbit:

$$E=-\frac{1}{2}m{v}^2$$

So, total energy = negative of kinetic energy.

---

(b)

The energy required to launch an orbiting satellite out of Earth’s gravitational influence is less than the energy required to project a stationary object at the same height out of Earth’s influence.

✔ An orbiting satellite already has kinetic energy, so additional energy needed is less.

---

Question 7.7

Does the escape speed of a body from the Earth depend on
(a) the mass of the body,
(b) the location from where it is projected,
(c) the direction of projection,
(d) the height of the location from where the body is launched?

---

Answer:

(a) Mass of the body:
❌ No
Escape speed is independent of the mass of the body.

(b) Location from where it is projected:
✔ Yes
Escape speed depends on the distance from the centre of the Earth.

(c) Direction of projection:
❌ No
Escape speed is independent of the direction of projection.

(d) Height of the point of projection:
✔ Yes
Escape speed decreases with increase in height above the Earth’s surface.

---

Question 7.8

A comet orbits the Sun in a highly elliptical orbit. Does the comet have a constant
(a) linear speed,
(b) angular speed,
(c) angular momentum,
(d) kinetic energy,
(e) potential energy,
(f) total energy
throughout its orbit?
(Neglect any mass loss of the comet when it comes very close to the Sun.)

---

Answer:

(a) Linear speed:
❌ No
The speed is maximum at perihelion and minimum at aphelion.

(b) Angular speed:
❌ No
Angular speed changes; it is higher when the comet is closer to the Sun.

(c) Angular momentum:
✔ Yes
Angular momentum remains constant because gravitational force is a central force.

(d) Kinetic energy:
❌ No
Kinetic energy varies with speed, so it is not constant.

(e) Potential energy:
❌ No
Gravitational potential energy depends on distance from the Sun and hence changes.

(f) Total energy:
✔ Yes
Total mechanical energy remains constant for an orbiting comet (bound system).

---

Question 7.9

Which of the following symptoms is likely to afflict an astronaut in space?
(a) swollen feet
(b) swollen face
(c) headache
(d) orientational problem

---

Answer:

✔ (b) Swollen face
✔ (d) Orientational problem

❌ (a) Swollen feet – Not likely, because in weightlessness body fluids move upward.
❌ (c) Headache – Not a typical direct effect of weightlessness.

---

Question 7.10

In the following two exercises, choose the correct answer from among the given ones:

The gravitational intensity at the centre of a hemispherical shell of uniform mass density has the direction indicated by the arrow (see Fig. 7.11):

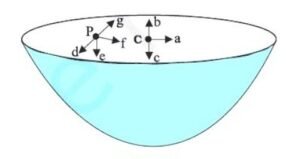
(i) a  (ii) b  (iii) c  (iv) 0

---

Answer:

✔ (ii) b

Explanation (exam-oriented):

• For a complete spherical shell, gravitational intensity at the centre is zero.

• In a hemispherical shell, mass is present only on one side.

• The gravitational pulls do not cancel completely.

• The resultant gravitational intensity is directed towards the curved surface of the hemisphere, along its axis of symmetry.

Hence, the correct direction is arrow b.

---

Question 7.11

For the above problem, the direction of the gravitational intensity at an arbitrary point P is indicated by the arrow:
(i) d  (ii) e  (iii) f  (iv) g

---

Answer:

✔ (iii) f

Explanation (brief):

• Gravitational intensity at any point is the resultant of attractions due to all mass elements.

• At an arbitrary point P near a hemispherical shell, components perpendicular to the axis partially cancel, while components towards the mass distribution dominate.

• The net gravitational intensity therefore points in the direction shown by arrow f.

---

Question 7.12

A rocket is fired from the Earth towards the Sun. At what distance from the Earth’s centre is the gravitational force on the rocket zero?
Mass of the Sun $=2\times {10}^{30}\text{kg}$,
Mass of the Earth $=6\times {10}^{24}\text{kg}$.
Neglect the effect of other planets.
Distance between Earth and Sun $=1.5\times {10}^{11}\text{m}$.

---

Answer:

Let the point where the net gravitational force is zero be at a distance $x$ from the centre of the Earth along the line joining Earth and Sun. At this point, gravitational attraction due to Earth equals that due to the Sun.

Step 1: Write force balance condition

$$\frac{G{M}_E}{x^2}=\frac{G{M}_S}{(R-x{)}^2}$$

Cancel $G$:

$$\frac{M_E}{x^2}=\frac{M_S}{(R-x{)}^2}$$

Step 2: Substitute values

$$\frac{6\times {10}^{24}}{x^2}=\frac{2\times {10}^{30}}{(1.5\times {10}^{11}-x{)}^2}$$

Taking square root on both sides:

$$\frac{\sqrt{6\times {10}^{24}}}{x}=\frac{\sqrt{2\times {10}^{30}}}{1.5\times {10}^{11}-x}$$

Step 3: Simplify

$$\frac{1.5\times {10}^{11}-x}{x}=\sqrt{\frac{2\times {10}^{30}}{6\times {10}^{24}}}=\sqrt{3.33\times {10}^5}\approx 577$$

$$1.5\times {10}^{11}-x=577x$$

$$1.5\times {10}^{11}=578x$$

$$x\approx \frac{1.5\times {10}^{11}}{578}\approx 2.6\times {10}^8\text{m}$$

---

Question 7.13

How will you “weigh the Sun”, that is, estimate its mass?
The mean orbital radius of the Earth around the Sun is
$1.5\times {10}^8\text{km}$.

---

Answer:

The mass of the Sun can be estimated using the motion of the Earth around the Sun and Newton’s law of gravitation.

---

Step 1: Use centripetal force condition

The gravitational force provided by the Sun acts as the centripetal force for Earth’s circular motion:

$$\frac{G{M}_{S}m}{R^2}=\frac{m{v}^2}{R}$$

where
$M_S$ = mass of the Sun,
$R$ = orbital radius of Earth,
$m$ = mass of Earth,
$v$ = orbital speed of Earth.

Step 2: Express velocity in terms of time period

$$v=\frac{2\pi R}{T}$$

Substitute in the force equation:

$$\frac{G{M}_S}{R^2}=\frac{4{\pi }^{2}R}{T^2}$$

$$M_S=\frac{4{\pi }^2{R}^3}{G{T}^2}$$

Step 3: Substitute numerical values

Mean orbital radius:

$$R=1.5\times {10}^8\text{km}=1.5\times {10}^{11}\text{m}$$

Time period of Earth:

$$T=1\text{year}=3.15\times {10}^7\text{s}$$

Gravitational constant:

$$G=6.67\times {10}^{-11}{\text{N m}}^2{\text{kg}}^{-2}$$

$$M_S=\frac{4{\pi }^2(1.5\times {10}^{11}{)}^3}{6.67\times {10}^{-11}(3.15\times {10}^7{)}^2}$$

$$M_S\approx 2.0\times {10}^{30}\text{kg}$$

---

Question 7.14

A Saturn year is 29.5 times the Earth year. How far is Saturn from the Sun if the Earth is
$1.50\times {10}^8\text{km}$ away from the Sun?

---

Answer:

Using Kepler’s Third Law:

$$\frac{T_S^2}{T_E^2}=\frac{R_S^3}{R_E^3}$$

where
$T_S=29.5T_E$,
$R_E=1.50\times {10}^8\text{km}$.

Step 1: Substitute values

$$(29.5{)}^2={\left(\frac{R_S}{R_E}\right)}^3$$

$$\frac{R_S}{R_E}=(29.5{)}^{2\mathrm{/}3}$$

Step 2: Calculate

$$(29.5{)}^{2\mathrm{/}3}\approx 9.55$$

Step 3: Find Saturn’s distance

$$R_S=9.55\times 1.50\times {10}^8$$

$$R_S\approx 1.43\times {10}^9\text{km}$$

---

Question 7.15

A body weighs 63 N on the surface of the Earth.
What is the gravitational force on it due to the Earth at a height equal to half the radius of the Earth?

---

Answer:

Weight on the surface of the Earth:

$$W=63\text{N}$$

Let the radius of Earth be $R$.
Given height:

$$h=\frac{R}{2}$$

Step 1: Use variation of gravity with height

Acceleration due to gravity at height $h$ is:

$$g_h=g{\left(\frac{R}{R+h}\right)}^2$$

Substitute $h=\frac{R}{2}$:

$$g_h=g{\left(\frac{R}{R+\frac{R}{2}}\right)}^2=g{\left(\frac{R}{\frac{3R}{2}}\right)}^2=g{\left(\frac{2}{3}\right)}^2=\frac{4g}{9}$$

Step 2: Find weight at height $h$

Since weight $W=mg$,

$$W_h=m{g}_h=m\left(\frac{4g}{9}\right)$$

But $mg=63\text{N}$, so:

$$W_h=\frac{4}{9}\times 63$$

$$W_h=28\text{N}$$

---

Question 7.16

Assuming the Earth to be a sphere of uniform mass density, how much would a body weigh half way down to the centre of the Earth if it weighed 250 N on the surface?

---

Answer:

Weight on the surface of the Earth:

$$W=250\text{N}$$

Let the radius of the Earth be $R$.

Halfway down to the centre means depth:

$$d=\frac{R}{2}$$

Step 1: Variation of gravity with depth

For a uniform-density Earth, acceleration due to gravity at depth $d$ is:

$$g_d=g(1-\frac{d}{R})$$

Substitute $d=\frac{R}{2}$:

$$g_d=g(1-\frac{1}{2})=\frac{g}{2}$$

Step 2: Find the weight at depth

Since weight $W=mg$,

$$W_d=m{g}_d=m\left(\frac{g}{2}\right)$$But $mg=250\text{N}$, therefore:

$$W_d=\frac{250}{2}=125\text{N}$$

---

Question 7.17

A rocket is fired vertically with a speed of 5 km s⁻¹ from the Earth’s surface. How far from the Earth does the rocket go before returning to the Earth?

Given:
Mass of Earth $M=6.0\times {10}^{24}\text{kg}$
Radius of Earth $R=6.4\times {10}^6\text{m}$
$G=6.67\times {10}^{-11}{\text{N m}}^2{\text{kg}}^{-2}$

---

Answer:

Initial speed of the rocket:

$$v=5{\text{km s}}^{-1}=5\times {10}^3{\text{m s}}^{-1}$$

At the highest point, the speed becomes zero.

Step 1: Use conservation of mechanical energy

Initial energy at Earth’s surface:

$$E_i=\frac{1}{2}m{v}^2-\frac{GMm}{R}$$

Final energy at maximum distance $r$:

$$E_f=-\frac{GMm}{r}$$

By energy conservation:

$$\frac{1}{2}m{v}^2-\frac{GMm}{R}=-\frac{GMm}{r}$$

Cancel $m$:

$$\frac{1}{2}{v}^2=GM(\frac{1}{R}-\frac{1}{r})$$

Step 2: Substitute values

$$\frac{1}{2}(5\times {10}^3{)}^2=(6.67\times {10}^{-11})(6.0\times {10}^{24})(\frac{1}{6.4\times {10}^6}-\frac{1}{r})$$
$$1.25\times {10}^7=4.002\times {10}^{14}(\frac{1}{6.4\times {10}^6}-\frac{1}{r})$$

$$\frac{1}{6.4\times {10}^6}-\frac{1}{r}=3.12\times {10}^{-8}$$

$$\frac{1}{r}=1.56\times {10}^{-7}-3.12\times {10}^{-8}=1.25\times {10}^{-7}$$

$$r=8.0\times {10}^6\text{m}$$

Step 3: Find height above Earth’s surface

$$h=r-R=(8.0-6.4)\times {10}^6$$

$$h=1.6\times {10}^6\text{m}$$

---

Question 7.18

The escape speed of a projectile on the Earth’s surface is 11.2 km s⁻¹. A body is projected with thrice this speed. What is the speed of the body far away from the Earth?
(Neglect the presence of the Sun and other planets.)

---

Answer:

Escape speed from Earth:

$$v_e=11.2{\text{km s}}^{-1}$$

Given initial speed:

$$v=3v_e=33.6{\text{km s}}^{-1}$$

Step 1: Use energy conservation

At Earth’s surface:

$$E_i=\frac{1}{2}m{v}^2-\frac{GMm}{R}$$

At infinity, gravitational potential energy is zero:

$$E_f=\frac{1}{2}m{v}_{\mathrm{\infty }}^2$$

For escape speed:

$$\frac{1}{2}m{v}_e^2=\frac{GMm}{R}$$

Step 2: Substitute $\frac{GM}{R}$

$$\frac{1}{2}m{v}^2-\frac{1}{2}m{v}_e^2=\frac{1}{2}m{v}_{\mathrm{\infty }}^2$$

Cancel $\frac{1}{2}m$:

$$v_{\mathrm{\infty }}^2=v^2-v_e^2$$

Step 3: Substitute values

$$v_{\mathrm{\infty }}^2=(3v_e{)}^2-v_e^2=9v_e^2-v_e^2=8v_e^2$$

$$v_{\mathrm{\infty }}=\sqrt{8}{v}_e=2\sqrt{2}{v}_e$$

$$v_{\mathrm{\infty }}=2\sqrt{2}\times 11.2\approx 31.7{\text{km s}}^{-1}$$

---

Question 7.19

A satellite orbits the Earth at a height of 400 km above the surface. How much energy must be expended to rocket the satellite out of the Earth’s gravitational influence?

Given:
Mass of satellite $m=200\text{kg}$
Mass of Earth $M=6.0\times {10}^{24}\text{kg}$
Radius of Earth $R=6.4\times {10}^6\text{m}$
Height $h=400\text{km}=4.0\times {10}^5\text{m}$
$G=6.67\times {10}^{-11}{\text{N m}}^2{\text{kg}}^{-2}$

---

Answer:

For a satellite in circular orbit, the total mechanical energy is:

$$E=-\frac{GMm}{2r}$$

where $r=R+h$

To escape Earth’s gravitational field, the total energy must be raised to zero.
Hence, energy required:

$$\mathrm{\Delta }E=0-E=\frac{GMm}{2r}$$

Step 1: Calculate orbital radius

$$r=R+h=6.4\times {10}^6+4.0\times {10}^5=6.8\times {10}^6\text{m}$$

Step 2: Substitute values

$$\mathrm{\Delta }E=\frac{(6.67\times {10}^{-11})(6.0\times {10}^{24})(200)}{2(6.8\times {10}^6)}$$

$$\mathrm{\Delta }E=\frac{8.004\times {10}^{16}}{1.36\times {10}^7}$$

$$\mathrm{\Delta }E\approx 5.9\times {10}^9\text{J}$$

---

Question 7.20

Two stars, each of one solar mass $(=2\times {10}^{30}\text{kg})$, are approaching each other for a head-on collision.
When they are at a distance of ${10}^9\text{km}$, their speeds are negligible. What is the speed with which they collide?

Radius of each star $={10}^4\text{km}$.(Assume the stars remain undistorted. Use the known value of $G$.)

---

Answer:

Given:
Mass of each star

$$M=2\times {10}^{30}\text{kg}$$

Initial separation

$$r_i={10}^9\text{km}={10}^{12}\text{m}$$

At collision, distance between centres

$$r_f=2R=2\times {10}^4\text{km}=2\times {10}^7\text{m}$$

Step 1: Use conservation of mechanical energy

Initially, kinetic energy is negligible, so total energy is purely gravitational potential energy:

$$E_i=-\frac{G{M}^2}{r_i}$$

At collision, both stars move with equal speed $v$.
Total kinetic energy:

$$K=2\times \frac{1}{2}M{v}^2=M{v}^2$$

Final potential energy:

$$E_f=-\frac{G{M}^2}{r_f}$$

Energy conservation:

$$M{v}^2=G{M}^2(\frac{1}{r_f}-\frac{1}{r_i})$$

Cancel $M$:

$$v^2=GM(\frac{1}{r_f}-\frac{1}{r_i})$$

Step 2: Substitute values

$$v^2=(6.67\times {10}^{-11})(2\times {10}^{30})(\frac{1}{2\times {10}^7}-\frac{1}{{10}^{12}})$$

Since

$$\frac{1}{{10}^{12}}\ll \frac{1}{2\times {10}^7},$$

we neglect the second term:

$$v^2\approx (6.67\times {10}^{-11})(2\times {10}^{30})\left(\frac{1}{2\times {10}^7}\right)$$

$$v^2\approx 6.67\times {10}^{12}$$

$$v\approx 2.58\times {10}^6{\text{m s}}^{-1}$$

---

Question 7.21

Two heavy spheres, each of mass 100 kg and radius 0.10 m, are placed 1.0 m apart on a horizontal table.
What is the gravitational force and gravitational potential at the mid-point of the line joining the centres of the spheres?
Is an object placed at that point in equilibrium? If so, is the equilibrium stable or unstable?

---

Answer

Given

• Mass of each sphere: $M=100\text{kg}$

• Distance between centres: $1.0\text{m}$

• Distance of midpoint from each centre:

  $$r=0.5\text{m}$$

• Gravitational constant:

  $$G=6.67\times {10}^{-11}{\text{N m}}^2{\text{kg}}^{-2}$$

(Outside a uniform sphere, gravity acts as if all mass were concentrated at the centre.)

---

(a) Gravitational force at the midpoint

Gravitational force on a test mass $m$ at the midpoint due to one sphere:

$$F_1=\frac{GMm}{r^2}$$

Both spheres exert equal forces in opposite directions.

$$F_{\text{net}}=F_1-F_1=0$$

$$\boxed{{\displaystyle F_{\text{mid}}=0}}$$

---

(b) Gravitational potential at the midpoint

Gravitational potential due to one sphere:

$$V_1=-\frac{GM}{\mathrm{r<span\; style="font-size:\; revert;\; font-family:\; var(--wp--preset--font-family--manrope);\; letter-spacing:\; -0.1px;"></span>}}$$

Total potential at midpoint (scalar addition):

$$V=V_1+V_1=-\frac{2GM}{r}$$

Substitute values:

$$V=-\frac{2(6.67\times {10}^{-11})(100)}{0.5}$$$$V=-2.67\times {10}^{-8}{\text{J kg}}^{-1}$$
$$\boxed{{\displaystyle V_{\text{mid}}=-2.67\times {10}^{-8}{\text{J kg}}^{-1}}}$$

(c) Nature of equilibrium

• Net gravitational force at the midpoint is zero, so the object is in equilibrium.

• If the object is displaced slightly towards one sphere, the nearer sphere pulls it more strongly.

• This causes the object to move further away from the midpoint.

$$\boxed{{\displaystyle \text{Equilibrium is unstable}}}$$