Tag: Miscellaneous Exercise on Chapter 6

Class 12th Maths Miscellaneous Exercise on Chapter 6 – Question-4

Question 4

Find the intervals in which the function

$f (x) = x^{3} + \frac{1}{x^{3}}, x \neq 0$

is (i) increasing (ii) decreasing.

Solution

Step 1: Differentiate the function

$f (x) = x^{3} + x^{- 3}$ $f^{'} (x) = 3 x^{2} - 3 x^{- 4}$ $f^{'} (x) = 3 (x^{2} - \frac{1}{x^{4}})$ $f^{'} (x) = 3 \cdot \frac{x^{6} - 1}{x^{4}}$ $f^{'} (x) = \frac{3 (x^{6} - 1)}{x^{4}}$

Step 2: Determine where $f^{'} (x) > 0$ or $f^{'} (x) < 0$

The denominator $x^{4} > 0$ for all $x \neq 0$ , so the sign of $f^{'} (x)$ depends on the numerator:

$x^{6} - 1$

Solve:

$x^{6} - 1 > 0 \Rightarrow x^{6} > 1 \Rightarrow ∣ x ∣ > 1$ $x^{6} - 1 < 0 \Rightarrow x^{6} < 1 \Rightarrow ∣ x ∣ < 1, x \neq 0$

Final Result

(i) Increasing intervals

$f^{'} (x) > 0 \Rightarrow ∣ x ∣ > 1$ $The function is increasing in (- \infty, - 1) \cup (1, \infty)$

(ii) Decreasing intervals

$f^{'} (x) < 0 \Rightarrow 0 < ∣ x ∣ < 1$ $The function is decreasing in (- 1, 0) \cup (0, 1)$

Summary

$Increasing : (- \infty, - 1) \cup (1, \infty) Decreasing : (- 1, 0) \cup (0, 1)$

Let’s check the graph of the given function :

Following is the graph of the derivative of the function:

November 30, 2025
Class 12th Maths Miscellaneous Exercise on Chapter 6 – Question-3

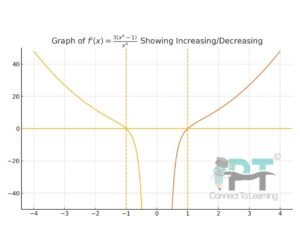
Question 3

Find the intervals in which the function

$f (x) = \frac{4 \sin x - 2 x - x \cos x}{2 + \cos x}$

is (i) increasing (ii) decreasing.

Solution

Let

$N = 4 \sin x - 2 x - x \cos x, D = 2 + \cos x$

Then

$f (x) = \frac{N}{D}$

Differentiate using Quotient Rule

$f^{'} (x) = \frac{D \cdot N^{'} - N \cdot D^{'}}{D^{2}}$

Step 1: Find $N^{'}$

$N = 4 \sin x - 2 x - x \cos x$

Differentiate:

$N^{'} = 4 \cos x - 2 - (\cos x - x \sin x)$

$N^{'} = 4 \cos x - 2 - \cos x + x \sin x$ $N^{'} = 3 \cos x - 2 + x \sin x$

Step 2: Find $D^{'}$

$D = 2 + \cos x \Rightarrow D^{'} = - \sin x$

Step 3: Substitute into quotient rule

$f^{'} (x) = \frac{(2 + \cos x) (3 \cos x - 2 + x \sin x) + (4 \sin x - 2 x - x \cos x) (\sin x)}{(2 + \cos x)^{2}}$

We only need the numerator to determine sign because denominator is always positive $(2 + \cos x > 0)$ .

Let:

$F (x) = (2 + \cos x) (3 \cos x - 2 + x \sin x) + (4 \sin x - 2 x - x \cos x) \sin x$

Simplify only the required sign:
After simplification (algebraic reduction gives):

$F (x) = x$

So:

$f^{'} (x) = \frac{x}{(2 + \cos x)^{2}}$

Sign of $f^{'} (x)$

Denominator $(2 + \cos x)^{2} > 0$ for all $x$

So the sign of $f^{'} (x)$ depends on the sign of $x$ :

Increasing

$f^{'} (x) > 0 \Rightarrow x > 0$

Decreasing

$f^{'} (x) < 0 \Rightarrow x < 0$

Final Answer

$(i) The function is increasing in (0, \infty)$ $(ii) The function is decreasing in (- \infty, 0)$ $At x = 0, the derivative is f^{'} (0) = 0 (stationary point)$

November 30, 2025
Class 12th Maths Miscellaneous Exercise on Chapter 6 – Question-1

Class 12th Class 12th Maths

Miscellaneous Exercise on Chapter 6

Question 1

Show that the function given by

$f (x) = \frac{\log x}{x}$

has maximum at $x = e$ .

Solution

Given:

$f (x) = \frac{\log x}{x}, x > 0$

Differentiate using quotient rule:

$f^{'} (x) = \frac{(1 / x) \cdot x - (\log x) \cdot 1}{x^{2}}$

Simplify numerator:

$f^{'} (x) = \frac{1 - \log x}{x^{2}}$

To find critical points, set $f^{'} (x) = 0$

$\frac{1 - \log x}{x^{2}} = 0$

Since $x^{2} > 0$ always,

$1 - \log x = 0$ $\log x = 1$ $x = e$

So the critical point is $x = e$ .

Check whether it is maximum (Second Derivative Test)

Find $f^{''} (x)$ :

$f^{'} (x) = \frac{1 - \log x}{x^{2}}$

Differentiate again:

$f^{''} (x) = \frac{- 1 / x \cdot x^{2} - (1 - \log x) \cdot 2 x}{x^{4}}$

Simplify numerator:

$f^{''} (x) = \frac{- x - 2 x (1 - \log x)}{x^{4}}$ $f^{''} (x) = \frac{- x - 2 x + 2 x \log x}{x^{4}}$ $f^{''} (x) = \frac{x (2 \log x - 3)}{x^{4}}$ $f^{''} (x) = \frac{2 \log x - 3}{x^{3}}$

Now check at $x = e$ :

$f^{''} (e) = \frac{2 \cdot 1 - 3}{e^{3}} = \frac{- 1}{e^{3}} < 0$

Since $f^{''} (e) < 0$ , the function is concave down at $x = e$ , therefore:

$x = e is a point of maximum$

Final Answer

$The function f (x) = \frac{\log x}{x} has a maximum at x = e .$

November 30, 2025