Question 21
Of all the closed cylindrical cans (right circular), of a given volume of 100 cubic centimetres, find the dimensions of the can which has the minimum surface area. Also draw the diagram.
Solution

Given:
A closed right circular cylinder with fixed volume
We want to minimize surface area (S):
From the volume formula:
Substituting into :
Differentiate w.r.t. :
Set derivative to zero:
Now find height:
Question 22
A wire of length 28 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the length of the two pieces so that the combined area of the square and the circle is minimum?
Solution
Let the total length of the wire = 28 m
Let the length of the wire used to form the square = meters
Then the length used for the circle = meters
For the Square
Perimeter of square =
Area of square:
For the Circle
Circumference =
Area of circle:
Total Area
To minimize area, differentiate w.r.t :
Set derivative = 0:
Cross-multiply:
Final Calculated Values
Wire used for the square:
Wire used for the circle:
Question 23
Prove that the volume of the largest cone that can be inscribed in a sphere of radius is of the volume of the sphere.
Solution
Consider a cone inscribed in a sphere of radius .
Let the height of the cone be and radius of its base be .
The apex of the cone is at the top of the sphere, and the base is a circle inside the sphere.
Using the figure
The centre of the sphere divides the height of the cone into two parts:
-
Distance from centre to base =
-
So remaining length (to apex) =
Thus, the height of the cone:
The base radius and form a right triangle with :
Volume of cone
Let:
Differentiate to find maxima
Expand:Differentiate:
Set derivative equal to zero:
Solve quadratic:
Positive solution:
Substitute back
Find :
So the radius .
Volume of the largest cone
Volume of sphere
Required ratio
Final Proof
Question 24
Show that the right circular cone of least curved surface and given volume has an altitude equal to times the radius of the base.
Solution
Let:
-
= radius of base of the cone
-
= height (altitude) of the cone
-
= slant height of the cone

Given volume is constant:
Curved surface area (lateral surface area) of cone:
We want to minimize
Express in terms of and
From right triangle:
So,
Using the volume constraint
Let (constant), then:
Substitute in surface area:
Differentiate to find minima
Let
Differentiate w.r.t :
Set :
Cross multiply:
Now find relation between and
Recall:
So:
From ,
Substitute:
Final Result
Question 25
Show that the semi-vertical angle of the cone of maximum volume and of given slant height is
Solution
Let:
-
= slant height of the cone (constant)
-
= radius of the base
-
= height of the cone
-
= semi-vertical angle of the cone
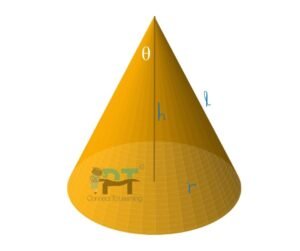
From geometry of the cone:
Volume of the cone
Substitute and :
Let:
Differentiate to maximize
Differentiate:
Set derivative = 0:
Factorize:
Divide both sides by :
Thus:
Final Result
Question 26
Show that the semi-vertical angle of a right circular cone of given surface area and maximum volume is
Solution
Let:
-
= radius of the base
-
= height
-
= slant height
-
= semi-vertical angle of the cone
From geometry of the cone:
Given: Total Surface Area is constant
Total surface area of a right circular cone:
Since is fixed, substituting :
Let , still constant:
So:where is constant.
Volume of cone
Substitute value of :
So:
for some constant .
Maximize
To maximize volume, maximize the function:
Take derivative . After simplification (standard calculus identity result):
Divide by :
Simplify using :
Solve
Final Answer
Thus, the semi-vertical angle of the cone which gives maximum volume for fixed surface area satisfies:
Question 27
The point on the curve which is nearest to the point (0,5) is
(A)
(B)
(C)
(D)
Answer: (A)
Solution
Curve:
Distance squared from to :
So or
Compute :
Nearest point is
Correct Answer = (A)
Question 28
For all real values of , the minimum value of
is
(A) 0 (B) 1 (C) 3 (D)
Solution
Let
This function is defined for all real because denominator never becomes zero:
Method: Using substitution
Let . Then rewrite numerator and denominator:
So
To find minimum, consider:
Take LCM:
Simplify numerator:
Since denominator > 0 for all real x and numerator ≥ 0:
Equality occurs when
Final Answer
Correct option: (D)
Question 29
The maximum value of
is
(A) (B) (C) (D)
Solution
Let
Simplify inside:
So:
Because cube root function is increasing, to maximize it is enough to maximize:
Consider g(x) on interval [0,1]
Set derivative = 0:
Check values at endpoints and critical point:
Maximum value
Final Answer
Correct option: (C) 1





