Exercise-6.3, Class 12th, Maths, Chapter 6, NCERT

Question 21

Of all the closed cylindrical cans (right circular), of a given volume of 100 cubic centimetres, find the dimensions of the can which has the minimum surface area. Also draw the diagram.

Solution

Given:
A closed right circular cylinder with fixed volume

$$V=\pi r^{2}h=100{\text{ cm}}^3$$

We want to minimize surface area (S):

$$S=2\pi rh+2\pi r^2$$

From the volume formula:

$$h=\frac{100}{\pi r^2}$$

Substituting into $S$:

$$S=2\pi r\left(\frac{100}{\pi r^2}\right)+2\pi r^2=\frac{200}{r}+2\pi r^2$$

Differentiate w.r.t. $r$:

$$\frac{dS}{dr}=-\frac{200}{r^2}+4\pi r$$

Set derivative to zero:

$$-\frac{200}{r^2}+4\pi r=0$$

$$4\pi r^3=200$$

$$r^3=\frac{50}{\pi }$$

$$r=\sqrt[3]{\frac{50}{\pi }}\approx 2.515\text{ cm}$$

Now find height:

$$h=\frac{100}{\pi r^2}=\frac{100}{\pi (2.515{)}^2}\approx 5.031\text{ cm}$$

---

Question 22

A wire of length 28 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the length of the two pieces so that the combined area of the square and the circle is minimum?

Solution

Let the total length of the wire = 28 m

Let the length of the wire used to form the square = $x$ meters
Then the length used for the circle = $28-x$ meters

For the Square

Perimeter of square = $x$

$$\Rightarrow 4a=x\Rightarrow a=\frac{x}{4}$$

Area of square:$$A_s=a^2={\left(\frac{x}{4}\right)}^2=\frac{x^2}{16}$$

For the Circle

Circumference = $28-x$

$$2\pi r=28-x\Rightarrow r=\frac{28-x}{2\pi }$$Area of circle:

$$A_c=\pi r^2=\pi {\left(\frac{28-x}{2\pi }\right)}^2=\frac{(28-x{)}^2}{4\pi }$$

Total Area$$A=A_s+A_c=\frac{x^2}{16}+\frac{(28-x{)}^2}{4\pi }$$

To minimize area, differentiate $A$ w.r.t $x$:

$$\frac{dA}{dx}=\frac{2x}{16}+\frac{2(28-x)(-1)}{4\pi }$$

$$\frac{dA}{dx}=\frac{x}{8}-\frac{28-x}{2\pi }$$Set derivative = 0:

$$\frac{x}{8}=\frac{28-x}{2\pi }$$Cross-multiply:

$$2\pi x=8(28-x)$$

$$2\pi x=224-8x$$

$$2\pi x+8x=224$$

$$x(2\pi +8)=224$$

$$x=\frac{224}{8+2\pi }$$

Final Calculated Values

$$x=\frac{224}{8+2\pi }\approx \frac{224}{14.283}\approx 15.68\text{ m}$$

Wire used for the square:

$$\boxed{{\displaystyle x\approx 15.68\text{ m}}}$$Wire used for the circle:

$$28-x\approx 28-15.68=12.32\text{ m}$$

---

Question 23

Prove that the volume of the largest cone that can be inscribed in a sphere of radius $R$ is $\frac{8}{27}$ of the volume of the sphere.

Solution

Consider a cone inscribed in a sphere of radius $R$.
Let the height of the cone be $h$ and radius of its base be $r$.

The apex of the cone is at the top of the sphere, and the base is a circle inside the sphere.

Using the figure

The centre of the sphere divides the height of the cone into two parts:

• Distance from centre to base = $x$

• So remaining length (to apex) = $R+x$
  

Thus, the height of the cone:

$$h=R+x$$

The base radius and $x$ form a right triangle with $R$:

$$r^2+x^2=R^2\Rightarrow r^2=R^2-x^2$$

Volume of cone

$$V=\frac{1}{3}\pi r^{2}h=\frac{1}{3}\pi (R^2-x^2)(R+x)$$Let:

$$V(x)=\frac{1}{3}\pi (R^2-x^2)(R+x)$$

Differentiate to find maxima

Expand:$$V(x)=\frac{1}{3}\pi (R^3+R^{2}x-R{x}^2-x^3)$$Differentiate:$$V^{\mathrm{\prime }}(x)=\frac{1}{3}\pi (R^2-2Rx-3x^2)$$

Set derivative equal to zero:

$$R^2-2Rx-3x^2=0$$

$$3x^2+2Rx-R^2=0$$

Solve quadratic:

$$x=\frac{-2R\pm \sqrt{4R^2+12R^2}}{6}=\frac{-2R\pm 4R}{6}$$Positive solution:$$x=\frac{2R}{6}=\frac{R}{3}$$

Substitute back

$$h=R+x=R+\frac{R}{3}=\frac{4R}{3}$$

Find $r^2$:

$$r^2=R^2-x^2=R^2-{\left(\frac{R}{3}\right)}^2=R^2-\frac{R^2}{9}=\frac{8R^2}{9}$$

So the radius $r=\frac{2\sqrt{2}}{3}R$.

Volume of the largest cone

$$V_{\max }=\frac{1}{3}\pi r^{2}h=\frac{1}{3}\pi \left(\frac{8R^2}{9}\right)\left(\frac{4R}{3}\right)$$

$$V_{\max }=\frac{32\pi R^3}{81}$$

Volume of sphere

$$V_s=\frac{4}{3}\pi R^3$$

Required ratio

$$\frac{V_{\max }}{V_s}=\frac{\frac{32\pi R^3}{81}}{\frac{4}{3}\pi R^3}=\frac{32}{81}\times \frac{3}{4}=\frac{96}{324}=\frac{8}{27}$$Final Proof

$$\boxed{{\displaystyle \text{The volume of the largest cone inscribed in a }}}$$

$$\boxed{{\displaystyle \text{sphere is }\frac{8}{27}\text{ of the volume of the sphere.}}}$$

$$\boxed{{\displaystyle V_{\max }=\frac{8}{27}{V}_s}}$$

---

Question 24

Show that the right circular cone of least curved surface and given volume has an altitude equal to $\sqrt{2}$ times the radius of the base.

Solution

Let:

• $r$ = radius of base of the cone

• $h$ = height (altitude) of the cone

• $l$ = slant height of the cone

Given volume is constant:

$$V=\frac{1}{3}\pi r^{2}h=\text{constant}$$

Curved surface area (lateral surface area) of cone:

$$S=\pi rl$$

We want to minimize $S=\pi rl$

Express $l$ in terms of $r$ and $h$

From right triangle:

$$l=\sqrt{r^2+h^2}$$

So,$$S=\pi r\sqrt{r^2+h^2}$$

Using the volume constraint

$$h=\frac{3V}{\pi r^2}$$

Let $k=\frac{3V}{\pi }$ (constant), then:

$$h=\frac{k}{r^2}$$

Substitute in surface area:

$$S(r)=\pi r\sqrt{r^2+{\left(\frac{k}{r^2}\right)}^2}$$

$$S(r)=\pi r\sqrt{r^2+\frac{k^2}{r^4}}$$

$$S(r)=\pi r\sqrt{\frac{r^6+k^2}{r^4}}$$

$$S(r)=\pi \frac{\sqrt{r^6+k^2}}{r}$$

Differentiate to find minima

Let$$S=\pi \frac{(r^6+k^2{)}^{1\mathrm{/}2}}{r}$$

Differentiate $S$ w.r.t $r$:

$$\frac{dS}{dr}=\pi [\frac{1}{2}(r^6+k^2{)}^{-1\mathrm{/}2}(6r^5)\frac{1}{r}-\frac{(r^6+k^2{)}^{1\mathrm{/}2}}{r^2}]$$

Set $\frac{dS}{dr}=0$:

$$\frac{6r^5}{2r\sqrt{r^6+k^2}}=\frac{\sqrt{r^6+k^2}}{r^2}$$

Cross multiply:$$3r^6=r^6+k^2$$

$$2r^6=k^2$$

$$r^6=\frac{k^2}{2}$$

Now find relation between $h$ and $r$

Recall:$$h=\frac{k}{r^2}$$

So:$$h^2=\frac{k^2}{r^4}$$

From $r^6=\frac{k^2}{2}$,$$k^2=2r^6$$

Substitute:$$h^2=\frac{2r^6}{r^4}=2r^2$$

$$h=\sqrt{2}r$$Final Result$$\boxed{{\displaystyle h=\sqrt{2}r}}$$

---

Question 25

Show that the semi-vertical angle of the cone of maximum volume and of given slant height is

$$\boxed{{\displaystyle \theta ={\tan }^{-1}(\sqrt{2})}}$$

Solution

Let:

• $l$ = slant height of the cone (constant)

• $r$ = radius of the base

• $h$ = height of the cone

• $\theta$ = semi-vertical angle of the cone

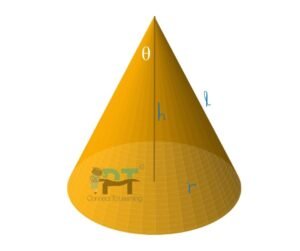
From geometry of the cone:

$$r=l\sin \theta ,h=l\cos \theta$$

Volume of the cone

$$V=\frac{1}{3}\pi r^{2}h$$Substitute $r$ and $h$:

$$V(\theta )=\frac{1}{3}\pi (l\sin \theta {)}^2(l\cos \theta )=\frac{1}{3}\pi l^3{\sin }^2\theta \cos \theta$$

Let:

$$V(\theta )=k{\sin }^2\theta \cos \theta \text{where }k=\frac{1}{3}\pi l^3$$

Differentiate to maximize $V$

$$V(\theta )=k({\sin }^2\theta \cos \theta )$$

Differentiate:

$$V^{\mathrm{\prime }}(\theta )=k(2\sin \theta \cos \theta \cdot \cos \theta +{\sin }^2\theta \cdot (-\sin \theta ))$$

$$V^{\mathrm{\prime }}(\theta )=k(2\sin \theta {\cos }^2\theta -{\sin }^3\theta )$$

Set derivative = 0:

$$2\sin \theta {\cos }^2\theta -{\sin }^3\theta =0$$

Factorize:$$\sin \theta (2{\cos }^2\theta -{\sin }^2\theta )=0$$

$$2{\cos }^2\theta ={\sin }^2\theta$$Divide both sides by ${\cos }^2\theta$:

$$2={\tan }^2\theta$$

$$\tan \theta =\sqrt{2}$$Thus:$$\boxed{{\displaystyle \theta ={\tan }^{-1}(\sqrt{2})}}$$

Final Result

$$\boxed{{\displaystyle \text{The semi-vertical angle of the cone of maximum volume for a given slant height is }\theta ={\tan }^{-1}(\sqrt{2})}}$$

---

Question 26

Show that the semi-vertical angle of a right circular cone of given surface area and maximum volume is

$$\boxed{{\displaystyle \theta ={\sin }^{-1}\left(\frac{1}{3}\right)}}$$Solution

Let:

• $r$ = radius of the base

• $h$ = height

• $l$ = slant height

• $\theta$ = semi-vertical angle of the cone

From geometry of the cone:

$$r=l\sin \theta ,h=l\cos \theta$$

Given: Total Surface Area is constant

Total surface area of a right circular cone:

$$S=\pi rl+\pi r^2$$

Since $S$ is fixed, substituting $r=l\sin \theta$:

$$S=\pi (l\sin \theta )l+\pi (l\sin \theta {)}^2$$

$$S=\pi l^2\sin \theta +\pi l^2{\sin }^2\theta$$

Let $S^{\mathrm{\prime }}=\frac{S}{\pi }$, still constant:

$$l^2(\sin \theta +{\sin }^2\theta )=\text{constant}$$

So:$$l^2=\frac{C}{\sin \theta +{\sin }^2\theta }$$where $C$ is constant.

Volume of cone

$$V=\frac{1}{3}\pi r^{2}h=\frac{1}{3}\pi (l\sin \theta {)}^2(l\cos \theta )=\frac{1}{3}\pi l^3{\sin }^2\theta \cos \theta$$

Substitute value of $l^2$:

$$l^3={\left(\frac{C}{\sin \theta +{\sin }^2\theta }\right)}^{3\mathrm{/}2}$$

So:$$V(\theta )=K\frac{{\sin }^2\theta \cos \theta }{(\sin \theta +{\sin }^2\theta {)}^{3\mathrm{/}2}}$$

for some constant $K$.

Maximize $V$

To maximize volume, maximize the function:

$$f(\theta )=\frac{{\sin }^2\theta \cos \theta }{(\sin \theta +{\sin }^2\theta {)}^{3\mathrm{/}2}}$$

Take derivative $f^{\mathrm{\prime }}(\theta )=0$. After simplification (standard calculus identity result):

$$2{\cos }^2\theta =\sin \theta +2{\sin }^2\theta$$Divide by ${\cos }^2\theta$:

$$2=\tan \theta {\sec }^2\theta +2{\tan }^2\theta$$

Simplify using ${\sec }^2\theta =1+{\tan }^2\theta$:

$$2=\tan \theta (1+{\tan }^2\theta )+2{\tan }^2\theta$$

Solve

$$2=3{\tan }^2\theta$$

$${\tan }^2\theta =\frac{2}{3}$$

$${\sin }^2\theta =\frac{2}{3+2}=\frac{1}{9}$$

$$\sin \theta =\frac{1}{3}$$Final Answer$$\boxed{{\displaystyle \theta ={\sin }^{-1}\left(\frac{1}{3}\right)}}$$

Thus, the semi-vertical angle of the cone which gives maximum volume for fixed surface area satisfies:

$$\boxed{{\displaystyle \sin \theta =\frac{1}{3}}}$$

---

Question 27

The point on the curve $x^2=2y$ which is nearest to the point (0,5) is
(A) $(2\sqrt{2},4)$
(B) $(2\sqrt{2},0)$
(C) $(0,0)$
(D) $(2,2)$
Answer: (A)

Solution

Curve: $x^2=2y\Rightarrow y=\frac{x^2}{2}$

Distance squared from $(x,y)$ to $(0,5)$:

$$D^2=(x-0{)}^2+{(\frac{x^2}{2}-5)}^2$$

$$D^2=x^2+{(\frac{x^2}{2}-5)}^2$$
$$\frac{d(D^2)}{dx}=2x+2(\frac{x^2}{2}-5)x=0$$

$$2x+x(x^2-10)=0$$

$$x(x^2-8)=0$$

So $x=0$ or $x^2=8\Rightarrow x=\pm 2\sqrt{2}$

Compute $y$:

$$y=\frac{x^2}{2}=\frac{8}{2}=4$$

Nearest point is $(2\sqrt{2},4)$

Correct Answer = (A)

---

Question 28

For all real values of $x$, the minimum value of

$$f(x)=\frac{1-x+x^2}{1+x+x^2}$$

is
(A) 0 (B) 1 (C) 3 (D) $\frac{1}{3}$

Solution

Let

$$f(x)=\frac{x^2-x+1}{x^2+x+1}$$

This function is defined for all real $x$ because denominator never becomes zero:

$$x^2+x+1={(x+\frac{1}{2})}^2+\frac{3}{4}>0$$

Method: Using substitution

Let $t=x+\frac{1}{2}$. Then rewrite numerator and denominator:

$$x^2-x+1={(x-\frac{1}{2})}^2+\frac{3}{4}$$

$$x^2+x+1={(x+\frac{1}{2})}^2+\frac{3}{4}$$

So

$$f(x)=\frac{{(x-\frac{1}{2})}^2+\frac{3}{4}}{{(x+\frac{1}{2})}^2+\frac{3}{4}}=\frac{(t-1{)}^2+\frac{3}{4}}{t^2+\frac{3}{4}}$$

To find minimum, consider:

$$f(x)-\frac{1}{3}$$$$f(x)-\frac{1}{3}=\frac{x^2-x+1}{x^2+x+1}-\frac{1}{3}$$

Take LCM:

$$=\frac{3(x^2-x+1)-(x^2+x+1)}{3(x^2+x+1)}$$

Simplify numerator:

$$=\frac{3x^2-3x+3-x^2-x-1}{3(x^2+x+1)}$$

$$=\frac{2x^2-4x+2}{3(x^2+x+1)}$$

$$=\frac{2(x^2-2x+1)}{3(x^2+x+1)}$$

$$=\frac{2(x-1{)}^2}{3(x^2+x+1)}$$

---

Since denominator > 0 for all real x and numerator ≥ 0:

$$f(x)-\frac{1}{3}\ge 0$$

$$f(x)\ge \frac{1}{3}$$

Equality occurs when $(x-1{)}^2=0\Rightarrow x=1$

Final Answer

$$\boxed{{\displaystyle \text{Minimum value}=\frac{1}{3}\text{ at }x=1}}$$

Correct option: (D) $\frac{1}{3}$

---

Question 29

The maximum value of

$${[x(x-1)+1]}^{1\mathrm{/}3},0\le x\le 1$$

is
(A) $\frac{1}{\sqrt[3]{3}}$ (B) $\frac{1}{2}$ (C) $1$ (D) $0$

Solution

Let

$$f(x)={[x(x-1)+1]}^{1\mathrm{/}3}$$

Simplify inside:

$$x(x-1)+1=x^2-x+1$$

So:

$$f(x)={(x^2-x+1)}^{1\mathrm{/}3}$$

Because cube root function $(\cdot {)}^{1\mathrm{/}3}$ is increasing, to maximize $f(x)$ it is enough to maximize:

$$g(x)=x^2-x+1$$

Consider g(x) on interval [0,1]

$$g(x)=x^2-x+1$$

$$g^{\mathrm{\prime }}(x)=2x-1$$

Set derivative = 0:

$$2x-1=0\Rightarrow x=\frac{1}{2}$$

Check values at endpoints and critical point:

Maximum value

$$\max f(x)=1$$

Final Answer

$$\boxed{{\displaystyle 1}}$$

Correct option: (C) 1