Class 12th Maths Miscellaneous Exercise on Chapter 6 – Question-12

Question 12.
Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius $r$is $\frac{4r}{3}$.

---

Solution

Let a right circular cone be inscribed in a sphere of radius $r$.
Place the sphere such that its centre is the origin $O(0,0)$.
Let the cone have vertex at the top of the sphere and base inside the sphere.

Let:

• $h$ = altitude (height) of the cone

• $x$ = radius of the base of the cone

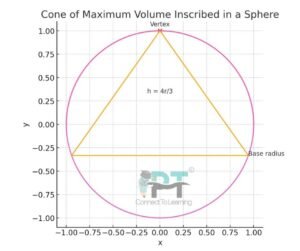
Since the cone is inside the sphere, its height extends from top of the sphere to some point on the vertical axis.

Consider the cross-section through the axis (a vertical diameter).
Let the vertex of the cone be at the top point of the sphere and the base centre lies somewhere inside.

So the height $h$ of the cone is measured downward from top.

The radius $x$ of the base relates to sphere radius using Pythagoras:

$$x^2+(r-h{)}^2=r^2$$
$$x^2=r^2-(r-h{)}^2$$
$$x^2=r^2-(r^2-2rh+h^2)$$
$$x^2=2rh-h^2$$

Volume of the cone

$$V=\frac{1}{3}\pi x^{2}h$$
$$V=\frac{1}{3}\pi (2rh-h^2)h$$
$$V=\frac{\pi }{3}(2r{h}^2-h^3)$$

Differentiate and find maximum

$$V=\frac{\pi }{3}(2r{h}^2-h^3)$$
$$V^{\mathrm{\prime }}=\frac{\pi }{3}(4rh-3h^2)$$

Set $V^{\mathrm{\prime }}=0$:

$$4rh-3h^2=0$$
$$h(4r-3h)=0$$

So:

$$h=0\text{or}4r-3h=0$$

Reject $h=0$ (no cone)

$$4r=3h$$
$$h=\frac{4r}{3}$$

Second derivative test

$$V^{\mathrm{\prime }\mathrm{\prime }}=\frac{\pi }{3}(4r-6h)$$

$$V^{\mathrm{\prime }\mathrm{\prime }}\left(\frac{4r}{3}\right)=\frac{\pi }{3}(4r-6\cdot \frac{4r}{3})=\frac{\pi }{3}(4r-8r)=\frac{\pi }{3}(-4r)<0$$

So $V$ is maximum at $h=\frac{4r}{3}$.

Answer

$$\boxed{{\displaystyle \text{The altitude of the right circular cone of maximum volume inscribed in a sphere of radius }r\text{ is }\frac{4r}{3}\mathrm{.}}}$$