Class 12th Maths Miscellaneous Exercise on Chapter 6 – Question-8

Question 8

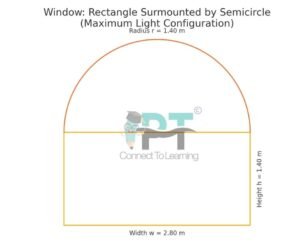
A window is in the form of a rectangle surmounted by a semicircle. The total perimeter of the window is 10 m.
Find the dimensions of the window so that the area is maximum (i.e., it admits maximum light).

---

Solution

Let

• $w=$ width of the rectangle (also diameter of the semicircle)

• $h=$ height of the rectangular part

• Radius of semicircle $r=\frac{w}{2}$

Perimeter Condition

The perimeter of the shape includes:

• top semicircle arc: $\frac{1}{2}(2\pi r)=\pi r=\frac{\pi w}{2}$

• two vertical sides: $2h$

• bottom width: $w$

So:$$w+2h+\frac{\pi w}{2}=10$$
$$2h=10-w-\frac{\pi w}{2}$$
$$h=\frac{10-w(1+\frac{\pi }{2})}{\mathrm{2<span\; style="font-size:\; revert;\; font-family:\; var(--wp--preset--font-family--manrope);\; letter-spacing:\; -0.1px;"></span>}}$$

Area of the Window

$$A=\text{Area of rectangle}+\text{Area of semicircle}=wh+\frac{1}{2}\pi r^2=wh+\frac{1}{2}\pi {\left(\frac{w}{2}\right)}^2$$
$$A=wh+\frac{\pi w^2}{8}$$

Substitute $h$:

$$A=w\left(\frac{10-w(1+\frac{\pi }{2})}{2}\right)+\frac{\pi w^2}{8}$$
$$A=\frac{w(10-w(1+\frac{\pi }{2}))}{2}+\frac{\pi w^2}{8}$$

Simplify:

$$A=5w-\frac{w^2}{2}(1+\frac{\pi }{2})+\frac{\pi w^2}{8}$$
$$A=5w-w^2(\frac{1}{2}+\frac{\pi }{4}-\frac{\pi }{8})$$
$$A=5w-w^2(\frac{1}{2}+\frac{\pi }{8})$$

Differentiate to Maximize Area

$$A^{\mathrm{\prime }}(w)=5-2w(\frac{1}{2}+\frac{\pi }{8})$$Set $A^{\mathrm{\prime }}(w)=0$:

$$5=w(1+\frac{\pi }{4})$$
$$w=\frac{5}{1+\frac{\pi }{4}}=\frac{20}{4+\pi }$$

Find $h$

$$h=\frac{10-w(1+\frac{\pi }{2})}{2}$$$$h=\frac{10-\frac{20}{4+\pi }(1+\frac{\pi }{2})}{\mathrm{2<span\; style="font-size:\; revert;\; font-family:\; var(--wp--preset--font-family--manrope);\; letter-spacing:\; -0.1px;"></span>}}$$

Simplify:

$$h=\frac{10-\frac{20\left(\frac{2+\pi }{2}\right)}{4+\pi }}{2}=\frac{10-\frac{10(2+\pi )}{4+\pi }}{2}$$
$$h=\frac{\frac{10(4+\pi )-10(2+\pi )}{4+\pi }}{2}=\frac{10(2)}{2(4+\pi )}=\frac{10}{4+\pi }$$

Final Dimensions

$$\boxed{{\displaystyle w=\frac{20}{4+\pi }\text{ m (width)}}}$$
$$\boxed{{\displaystyle h=\frac{10}{4+\pi }\text{ m (height of rectangle)}}}$$
$$\boxed{{\displaystyle r=\frac{w}{2}=\frac{10}{4+\pi }\text{ m (radius of semicircle)}}}$$

Conclusion

$$\boxed{{\displaystyle \text{The area is maximum when the radius of the semicircle equals the height of the rectangle.}}}$$
$$\boxed{{\displaystyle h=r}}$$